前言

深入DL领域读论文是必不可少的工作(其实我还有别的原因)，本意是开个好头吧，然后主要是学习最新的思想，开拓下自己的眼界。我觉得论文研读主要是从翻译、理解、算法实现、实验几个方面下手。

最近研读的是Accelerating Very Deep Convolutional Networks for Classfication and Dectection，作者主要对“超深层网络”(文中对SPP-10和VGG-16两种模型进行了实验)通过通道维度上的分解，达到加速的目的，并且提出了优化算法，显著降低了由于低秩分解带来的损失。

研读

主要包含一些重点的原文翻译、理解和引申思考。

引言与必要性

这里简单地说一下必要性和实际意义。

ML，DL领域的模型主要是训练和用其进行预测，这算是模型最基本的两个要素。一般来说预测的开销要远低于训练，人们对预测的开销的关注也高于训练的，因为在某些实际应用中，预测必须能在规定的时间内快速响应，或者是模型的预测必须要运行在较低计算能力的处理器上（比如移动设备）等。DL中的卷积神经网络(CNNs)在图像识别领域取得了巨大的成功，尤其是一些深层网络，比如VGG，ResNet等，其在ImageNet上预训练的模型也时常被用做图像特征的提取器。但是实际中由于网络层次的增加，整个网络的运行时间也随之增加，而且我们可以发现，运行CNNs时，其花销在卷积层上的时间可以达到90%以上(在VGG-16上的运行测试可以发现)。这限制了CNNs的应用，尤其是在移动设备、图像特征提取器方面。从卷积层方面加速CNNs是一个很好的课题。而原文的研究正是针对深层的CNN网络的test时间的加速。

原文的相关工作一节中还提到，加速过程由两个重要的部分组成：(i)一种降低时间复杂度的层分解方法。(ii)分解设计的优化算法（即优化分解后得到的参数，使得它最大程度地近似原有的输出）。

线性加速方法

线性加速方法基于这样一种假设：每一层卷积层的输出近似地属于一种低秩子空间。如果我们用低秩子空间的近似输出 y′y^{\prime} 来近似替代原有的输出 yy，并且将原有的得到 y{y} 的卷积过程，替换成得到低秩近似输出的 y′{y^{\prime}} 的卷积过程，那么由于 y′{y^{\prime}} 的低秩性，替换的过程的复杂度就有可能减少。

在这里，我们考虑包含 d{d} 个大小为 k×k×c{k\times k\times c} 的卷积核的卷积层，其中 k{k} 为卷积核的空间大小，c{c} 是该层的输入通道个数，并使用 W∈Rk2c{W \in \mathbf{R}^{k^{2}c}} 表示该卷积层的权重。我们使用 x∈Rk2c{x \in \mathbf{R}^{k^{2}c} } 表示单次卷积运算的输入，它的大小与卷积核大小相等。我们将 W{W} 和 x{x} 展开成列向量，并再添加一维输入作为常数的bias，即 W,b∈Rk2c+1{W,b \in \mathbf{R}^{k^{2}c+1}}。则某一层某一点的输出 y∈Rd{y \in \mathbf{R}^{d}} 可以由以下公式计算得到：

y=Wx{y=Wx}

记上式为式(1)。假设向量 yy 位于一个低秩子空间，则我们可以把它写成 y=M(y−y‾)+y‾{y=M(y-\overline{y})+\overline{y}}，其中 MM 是 d×d{d \times d} 的大小的矩阵，y‾{\overline{y}} 是输出的均值向量。扩展这个公式，我们可以通过以下公式计算输出：

y=MWx+by=MWx+b

记上式为式(2)，它描述了在原有的卷积方法上如何计算得到近似输出，其中式中的 b=y‾−My‾{b=\overline{y}-M{\overline{y}}} 为新的bias。进一步，秩为 d′{d^{\prime}} 的矩阵 MM 可以分解为两个d×d′{d \times d^{\prime}}的矩阵 PP 和 QQ ，则有 M=PQT{M=PQ^T}。我们记 W′=QTW{W^{\prime}=Q^{T}W}，它是一个 d′×(k2c+1){d^{\prime}\times(k^{2}c+1)} 的矩阵，可以把它看成一组新的大小为 d′{d^{\prime}} 的卷积核，那么我们可以用以下公式计算(2)式:

y=PW′x+by=PW^{\prime}x+b

记上式为式(3)，该公式就相当于新的卷积过程，使用它计算得到 yy 的计算输出的时间复杂度是O(d′k2c)+O(dd′){O(d^{\prime}k^{2}c)+O(dd^{\prime})}，而使用公式(1)(即原有的卷积过程)的复杂度是O(dk2c){O(dk^{2}c)}。对于许多典型的网络或卷积层，我们通常有O(dd′)≪O(d′k2c){O(dd^{\prime})}\ll O(d^{\prime}k^{2}c)，所以使用公式(3)理论上可以将时间复杂度降至d′/d{d^{\prime}/d}。

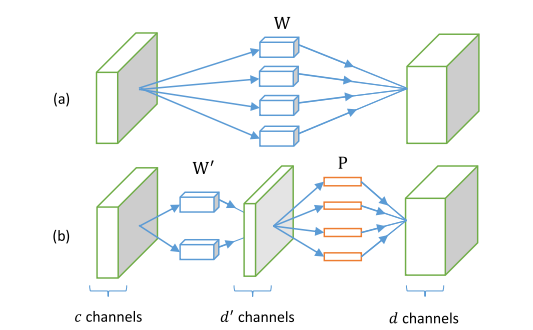
分解的卷积层图
分解的卷积层图

上图形象地描述了使用公式(3)对实际网络的分解效果，我们将使用两层网络替换原有的网络，他们分别由参数 W′,P{W^{\prime},P}(分解后的卷积层) 和 W{W}(原卷积层) 给定。矩阵 W′{W^{\prime}} 实际上表示大小为 k×k×c{k\times k\times c} 的 d′{d^{\prime}} 个卷积核。这些卷积核将输出 d′{d^{\prime}} 维的特征映射向量。d′×d{d^{\prime}\times d} 大小的矩阵 P{P} 可以表示为大小为 1×1×d′{1\times 1\times d^{\prime}} 的 d{d} 个卷积核。它将前卷积层 W′{W^{\prime}} 的 d′{d^{\prime}} 维的特征映射重新卷积成 d{d} 维的输出，这样分解得到的两层卷积层的输出与原有的卷积层输出是相同的。

注意到矩阵 M{M} 的分解方法 M=PQT{M=PQ^{T}} 可以是任意的。这不会影响公式(3)计算的 y{y} 的值。一种简单的分解方法是特征值分解方法(SVD)，即: M=Ud′Sd′Vd′T{M=U_{d^{\prime}}S_{d^{\prime}}V_{d^{\prime}}^{T}}，其中 Ud′{U_{d^{\prime}}} 和 Vd′{V_{d^{\prime}}} 是 d×d′{d\times d^{\prime}} 大小的列特征向量组成的矩阵， Sd′{S_{d^{\prime}}} 是 d′×d′{d^{\prime} \times d^{\prime}} 的对角矩阵。那么我们就可以得到 P{P} 和 Q{Q} 的公式： P=Ud′S1/2_d′{P=U_{d^{\prime}}S^{1/2}\_{d^{\prime}}} 和 Q=Vd′S1/2_d′{Q=V_{d^{\prime}}S^{1/2}\_{d^{\prime}}}。

以上的部分解决了前述的分解问题，以下是针对近似的层参数的最优解的计算过程。

事实上，前述的低秩假设并不能严格成立，所以公式(3)的计算只是近似的。为了找到一个合适的低秩近似子空间，我们将优化以下问题：

min⁡M∑i∣∣(yi−y‾)−M(yi−y‾)∣∣22\min \limits_{M} \sum_{i}{||(y_{i}-\overline{y}) - M(y_{i}-\overline{y})||^{2}_{2}}

s.t.rank(M)≤d′{s.t.\qquad rank(M)\le d^{\prime}}

这里的 yi{y_{i}} 是从测试集的特征映射中采样得到的。此问题可以由SVD或者主成成分分析(PCA)求解:

将n{n}个输出(列向量)分别减去它们的均值，按列连接转置后得到 Y{Y}，并计算它的协方差矩阵的特征分解：YYT=USUT{YY^{T}=USU^{T}}，其中式中的 U{U} 是一个正交阵，S{S} 为对角阵，于是我们可以得到 M=Ud′Ud′T{M=U_{d^{\prime}}U_{d^{\prime}}^{T}}，其中 Ud′{U_{d^{\prime}}} 是最大的 d′{d^{\prime}} 个特征特征对应的特征向量。从上面 M{M} 的计算过程来看，我们最终可以得到 P=Q=Ud′{P=Q=U_{d^{\prime}}}。

以上的线性分解过程翻自原文3.1小节，为了理解略有改动，图为原文的Fig1。

理解

  1. 低秩假设的合理性

    卷积元素是线性的，因此有矩阵乘法的秩的公式：

    rank(Wx)≤min⁡(rank(W),rank(x)){rank(Wx) \leq \min (rank(W), rank(x)) }

    由公式(1)和以上的式子，我们可以很容易得到：输出 yy 的低秩性源于输入 xx 的低秩性和卷积核 WW 的低秩性。由于卷积的特性，相邻的输入 x{x} 有重叠的部分，而且当步长为1时，对大小为 k×k×c{k \times k \times c} 的卷积核而言，最大重叠率为 k−1k{\frac{k-1}{k}}，这表明了不同区域的输入 x{x} 之间的信息的冗余。而且，对有意义的图像而言，它总是具有低秩性，这表明了 x{x} 本身的信息冗余。从卷积核的角度来说，对某些简单的卷积核而言，它具有的形式也是低秩的。

  2. 低秩假设和层分解的关系？

    这一点已经在该节开头的假设部分提出。但是令人非常感兴趣的是它是如何和通道维度的分解相关联的？我觉得这一点是由他们对 xx 的展开形式、卷积核的形式和公式的形式决定的。

  3. 引申和扩展，除了卷积输出的低秩性，能否利用输入和卷积核的低秩性提出新的方法？

    输入 xx 的低秩性是由其表示的实际意义决定，但是对它的近似可能并不会那么有效，主要原因是这种近似是由输入决定的，而输入的多样性对于模型本身是未知的。这将导致：(i)不同的输入近似的效果是由输入本身决定的，我们很难控制加速应有的效果。(ii)不同的输入有其自己的近似过程，这表示很难有一种固定的近似方法对所有输入有效，这种近似过程的计算是在test过程完成的，视feature map的大小会增加test的时间。

  4. 引申：
    输入的低秩性:

我们考虑总体的公式，而非单个输入 xx ，我们使用 x1,x2,…,xmx_{1}, x_{2}, \ldots, x_{m} 表示卷积过程一张图片的所有输入（mm的具体大小与卷积核的大小、步长等有关，它的计算公式将在之后给出），并记 X=(x1,x2,…,xm)X = (x_{1}, x_{2}, \ldots, x_{m}) 其中 xix_{i} 如前述的公式也展开成大小为 (k2c+1)×1(k^{2}c+1) \times 1 的列向量。使用前述的相同定义 W∈Rd×(k2+1){W \in \mathbf{R}^{d \times (k^{2} + 1)}} 表示卷积核，则feature map可以由以下公式计算得到：

y=WX{ y = WX }

其中 yy 是大小为 d×md \times m 的feature map。 记 X′X^{\prime} 是 XX 的降维后的结果， X′X^{\prime} 的大小为 (k2c+1)×t{(k^{2}c+1) \times t}，其中 t≤m{t \leq m}，并且有从 X′{X^{\prime}} 恢复至 X{X} 的变换：X=X′M{X = X^{\prime}M}，则上式就可以变成：

y=WX′M{ y = W X^{\prime} M }

该式子的意义是将原有的 X{X} 低秩近似成 X′{X^{\prime}}， 它将减少卷积的运算，而 M{M} 是将卷积得到的输出恢复填充到原有的大小。不考虑 M{M} 的与运算时间，那么卷积计算将减少到原有的t/m{t/m}。

未完待续…\ldots

参考文献

[1] Xiangyu Zhang, Jianhua Zou, Kaiming He, Jian Sun, “Accelerating Very Deep Convolutional Networks for Classification and Detection” arXiv:1505.06798