Preface 前言
SVD (Singular Value Decomposition) 在机器学习等其他领域有着非常广泛的应用,本文主要是受到计算机图像学课和以前看到的材料的启发,希望对SVD有更深入的了解。
相关的pdf资料可以参见我github上的记录。本文行文基本上是对它的翻译和理解。
Preparation
我们先叙述一些名词和涉及到的线性代数中的一些看法。
非齐次线性方程组Ax=b的计算可以有两种形式,这取决于我们对矩阵具体含义的看法。
如计算:
[1−332]×[31]
我们一般习惯的计算方式是row-way:ai,j是左矩阵的i行和右矩阵的j列对应相乘求和,即:
[1−332]×[31]=⎣⎢⎢⎡[13]×[31][−32]×[31]⎦⎥⎥⎤=[67]
column-way将矩阵看成列向量组,我们得到的结果b就是列向量组的线性组合,系数为x。
[1−332]×[31]=3×[1−3]+1×[31]=[67]
Column-Way使得我们将求解非齐次线性方程组Ax=b看成用列向量组A表出b,如果:
- b在列向量组张成的空间中,则我们一定可以求得x,它是表出的系数。
- b不在列向量组张成的空间中,我们希望求得它的最小二乘解。
Anotations
我们给出四个特殊的名词。
Perpframes(正交标架)
Perpframe一词源于Perpendicular(垂直)和frame(框架)。更好的理解的说法是orthonormal basis(单位正交基)。我们给定一组单位正交基[v0,v1,⋯,vn],它满足:
{viTvj=0viTvj=1i=ji=j
以下我们使用一组二维平面的单位正交基[v1,v2]来叙述。
Aligners
上述的单位正交基对应的Aligners 定义为:
[v1Tv2T]
它具有如下的性质:
[v1Tv2T]⋅v1=[v1T⋅v1v2T⋅v1]=[10][v1Tv2T]⋅v2=[v1T⋅v2v2T⋅v2]=[01]
也就是说,Aligners将单位正交基投影到x-y坐标轴(即二维平面的标准正交基[e1,e2])。
Hangers
上述的单位正交基对应的Hangers定义为:
[v1,v2]
它具有的性质是:
[v1,v2]⋅[01]=v2[v1,v2]⋅[10]=v1
也就是说,Hangers的作用正好和Aligners相反,它把标准正交基投影到我们的单位正交基上。
同时我们注意到:
Aligners⋅Hangers=[v1Tv2T]⋅[v1v2]=[1001]=E
这说明:同一组单位正交基的Aligners和Hangers是互逆的。
Stretchers(伸缩)
Stretchers比较好理解,它是对角阵:
Stretchers=diagnal(λ0,λ1,⋯,λn)
如R2上的一个Stretchers定义为:
[a00b]
对任意二位平面内的向量[x,y]T,Stretchers对它进行变换有:
[a00b]⋅[xy]=[axby]=x⋅[a0]+y⋅[0b]
[a0]=a⋅[10]=a⋅e1[0b]=b⋅[01]=b⋅e2
即Stretchers对应位置上的值对对应维度上的单位正交基进行了放缩。
Coordinate(坐标)
对任意二维平面上的向量p=[x1,x2]T,首先我们要理解这里给出的坐标实际是p在标准正交基下的坐标,如果我们想求它在单位正交基[v1,v2]下的坐标:
p=av1+bv2=[v1,v2]⋅[ab]=[e1,e2]⋅[x1x2]
我们用Aligners左乘上面的式子得到:
Aligners⋅p=[v1Tv2T][v1,v2]⋅[ab]=[ab]
上面的式子里[v1,v2]=Hangers,则:
[v1,v2]⋅[ab]=[x1x2]=p
我们从以上可以看出:
- Aligners将向量在标准正交基上的坐标变换到它的单位正交基上的坐标。
- Hangers将向量在它的单位正交基上的坐标变换到标准正交基上的坐标。
Example (例子)
给定二维平面上的一组单位正交基:
⎩⎪⎨⎪⎧v1=[22,22]Tv2=[−22,22]T
求向量p=[3,5]T到v1的垂足。
解:
p在x-y轴上对于x轴上的垂足我们很容易得到是[3,0],我们只需要令y轴的坐标为0,也就是说我们将一个Stretchers作用于p:
[1000]⋅p=[30]
这个Stretchers保持p在x轴的伸缩尺度为1,在y轴的伸缩尺度为0。
那我们的思路可以是:将p变换到给定的单位正交基上,用该Stretchers作用它,得到垂足在单位正交基上的坐标,再将其变换回x-y坐标系,一系列的变换矩阵A为:
A⋅p=(Hangers)⋅(Stretchers)⋅(Aligners)⋅p=[2222−2222]⋅[1000]⋅[22−222222]⋅[35]=[44]
这就是整个的变换过程,也是计算机图像学中几个变换矩阵连续变换的理论,将复杂的变换分解有利于计算。
Singular Value Decomposition (SVD分解)
SVD分解就是这样一个命题:对任意一个m×n的矩阵A,存在以下的分解形式:
A=(Hangers)⋅(Stretchers)⋅(Aligners)
SVD的精妙之处在于:它对任意的矩阵都成立,任意的矩阵都有如上的分解形式。
问题是我们如何找到这样的(Hangers)(Stretchers)(Aligners)。
构造
首先,对任意一个m×n的矩阵A,我们可以将它看成是Rn→Rm的变换(线性映射)。我们可以在Rn里找到一组单位正交基[a1,a2,⋯,an],而且这样的单位正交基有任意多个。
我们将这组单位正交基通过A投影到另一组向量[d1,d2,⋯,dn](注意该向量组共有n个元素,每个元素是m维)。
我们定义标量si=∣∣di∣∣=∣∣Aai∣∣。
由此我们定义另一组向量 [h1,h2,⋯,hn],它们满足:
hi={0si1Aaiifsi=0ifsi=0
我们可以发现以下的式子成立:
H⋅S⋅A′=[h1,h2,⋯,hn]⋅⎣⎢⎢⎡s1s2⋱sn⎦⎥⎥⎤⋅⎣⎢⎡a1T⋮anT⎦⎥⎤=[Aa1,Aa2,⋯,Aan]⋅⎣⎢⎡a1T⋮anT⎦⎥⎤=A[a1,a2⋯,an]⎣⎢⎢⎢⎡a1Ta2T⋮anT⎦⎥⎥⎥⎤=A
特别注意的是以上的矩阵的大小:
H的大小为m×n,S的大小为n×n,是一个对角阵,同时是一个Stretchers;A′的大小为n×n,同时是一个Aligner。只有H不一定是Hanger。
基于以上的构造方法,我们发现现在的问题是:寻找合适的Rn空间的单位正交基[a1,a2,⋯,an]使得通过以上构造方法得到的H为Hanger,那我们就得到了对一个矩阵进行SVD分解的三个矩阵,同时证明了任意一个矩阵有SVD分解。
构造Hanger
得到单位正交向量组
要使得向量组[h1,h2,⋯,hn]构成Hanger,当且仅当该向量组也是一组单位正交基。
对任意hi,根据之前的si的定义,只要si=0,我们有:
hi⋅hi=si21∣∣Aai∣∣2=1
剩下的关键就是如何使得hi正交,即
hi⋅hj=0if(i=j)
我们如下推导:
hi⋅hj=Aai⋅Aaj=aiT(ATAaj)=(Aai)TAaj=0
我们只要令:
ATAaj=λaj
就可以使得:
aiT(ATAaj)=aiTλaj=0=hihjif(i=j)
通过上面的推导,我们发现这唯一的一组正交基正是ATA的特征向量[a1,a2,⋯,an]。而且由于ATA是实对称阵,[a1,a2,⋯,an]一定存在,通过它得到的向量组[h1,h2,⋯,hn]一定是正交的。
这里我们还有最后一个问题,向量组[h1,h2,⋯,hn]是否是Rm的基。
基的讨论
首先,由矩阵秩的不等式:
rank(ATA)≤min(rank(AT),rank(A))=rank(A)≤min(m,n)
如果m=n,矩阵ATA一定不是满秩,则它一定存在λ=0的特征值,且由于矩阵ATA可分解,它的特征值的几何重数等于代数重数,该特征值对应的特征向量的个数等于n−rank(ATA)。我们把这些特征向量记作ci,其中i=1,⋯,n−rank(ATA)。
对ci,我们有:
ATAci=0
则
ciTATAci=0=∣∣Aci∣∣
又根据si的定义,我们知道这些ci对应的hi=Aci都是零向量。也就是说向量组[h1,h2,⋯,hn]中必定存在至少n−rank(ATA)个零向量。
又
n−rank(ATA)≥n−rank(A)≥n−min(m,n)
我们下面分析m,n的大小的两种情况:
-
m<n
此时矩阵A就是高维空间向低维空间的映射,它完成了降维的功能。
如果m<n,那么向量组[h1,h2,⋯,hn]中必定存在至少n−m个零向量,我们把这些零向量去除,得到至多包含m个向量的向量组[h1,h2,⋯,hm]。
如果A的秩为m,那么向量组[h1,h2,⋯,hm]中就不再包含零向量。该向量组包含m个向量,每个向量又是m维的,那么该向量组一定是Rm的基。
如果A的秩小于m,那么向量组[h1,h2,⋯,hm]中仍有零向量,我们仍将他们去除,变成[h1,h2,⋯,hk],我们将该向量组扩充,向该向量组添加m−k个互相正交的向量,得到的新的向量组[h1,h2,⋯,hm]就构成Rm的基。
-
m≥n
此时矩阵A是升维功能。
此时的分析过程大致和上面的情况相同,向量组[h1,h2,⋯,hn]中必定包含至少0个零向量,如果A的秩小于n,我们仍然将对应的零向量去除。无论是否去除零向量,如果向量组中向量的个数小于m,我们仍添加正交的向量使整个向量组包含m个正交向量,这样得到Rm的基。
总结一下就是:使用之前的构造方法必然得到至多m个正交向量hi,如果向量组个数小于m,我们就扩充该向量组,这样必然可以得到Rm的基。
而且,因为这些扩充的向量对应的si是0,所以这样的H和S,A′相乘时仍然可以还原成A。
这里还有一个比较值得我们注意的是在SVD分解中三个矩阵的大小,在我们最初的构造过程中我们得到的分解模式
A=H⋅S⋅A′
H的大小为m×n,S的大小为n×n,A′的大小是n×n。
如果我们去掉H列向量组中的零向量,对应的我们去除S中对应的行,我们得到的矩阵大小现在是:H的大小为m×k,S的大小为k×n。
我们按照前述的得到Rm的基的方法,如果k<m就添加正交向量将H列向量组扩充为m个,并在S的相应位置添加全零行。我们现在得到的矩阵大小是:H的大小为m×m,S的大小为m×n,A′的大小是n×n。这就得到了我们想要的满足SVD定义的标准分解。
关于SVD最后想说的几点
- Stretcher矩阵的大小和矩阵A大小相等。
The dimensions of the stretcher matrix will always match the dimensions of A.
- 对应关系:Hanger矩阵的第i列,对应Stretcher矩阵的第i行。Stretcher矩阵的第i列,对应Aligner矩阵的第i行。(废话)也就是如果要删去行列,要遵守这一规则,这将在PCA中有用。
Application of SVD
限于篇幅,有关于SVD分解的应用将在另外的文章中叙述。
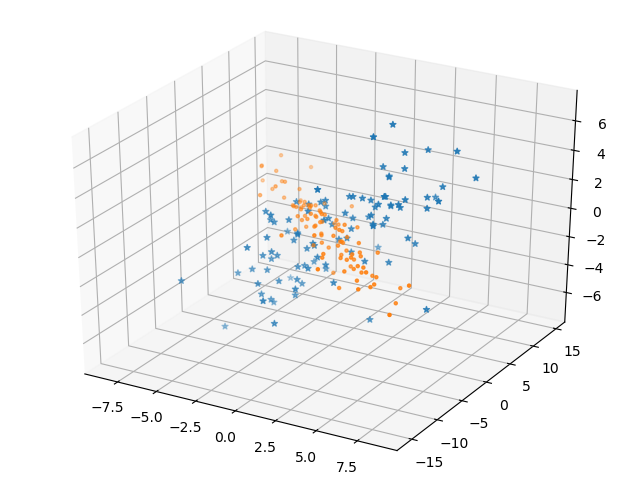
比如下面是一个SVD分解的例子,任意给定一个3×3的矩阵,它将三维空间的样本变换到相同的三维空间上。
任意三维空间的变换
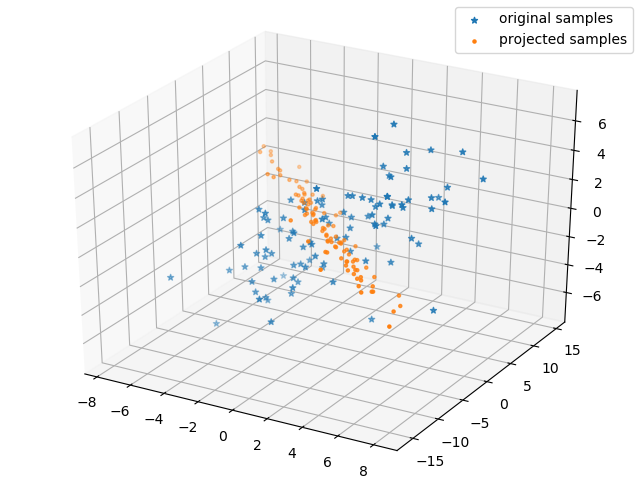
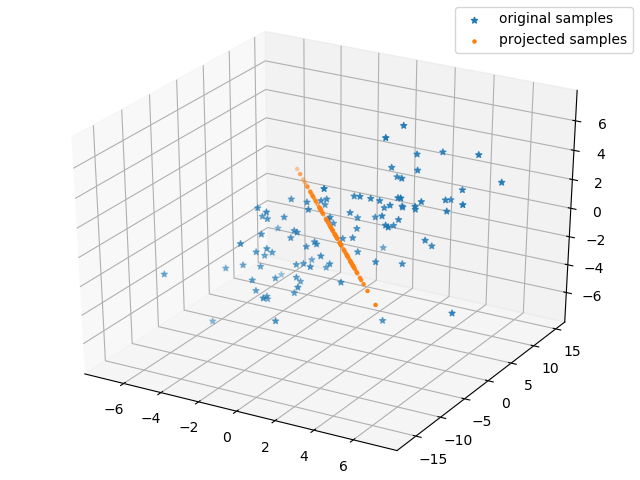
但是如果我们对它进行SVD分解,再去掉相应的维度的变换,就可以降低该矩阵的维度,使他将样本变换到二维空间,甚至是一维空间,这就是矩阵降秩(或者说矩阵低秩近似)问题。
以下就是将该矩阵降秩到二和一的情况。
降秩到二
降秩到一