KL divergence(KL 散度)

KL散度(Kullback-Leibler (KL) divergence)通常用来衡量两个单独的概率分布的差异，设对于同一随机变量的两个概率分布为P(x){P(x)}和Q(x){Q(x)}，则它们的KL散度定义为：

DKL(p∣∣q)=Ex∼P[log⁡P(x)−log⁡Q(x)]{ D_{KL}(p \vert \vert q) = \mathbb{E}_{x\sim P} \left[ \log P(x) - \log Q(x) \right] }

KL散度具有的性质有：

  • 非负：要使得KL散度为0，当且仅当P(x){P(x)}和Q(x){Q(x)}是在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是“几乎处处”相同的[1]。
  • 非对称：对某些P(x){P(x)}和Q(x){Q(x)}，KL散度和逆KL散度通常并不相等，也就是DKL(P∣∣Q)≠DKL(Q∣∣P){D_{KL}(P\vert\vert Q) \neq D_{KL}(Q \vert \vert P)}。

本文将从三个角度分析KL散度的非对称性：直观看法，理论说明，计算实验。

KL散度的非对称性

直观看法

假设在问题中，我们已知某种分布P(x){P(x)}，我们希望使用分布Q(x){Q(x)}来近似P(x){P(x)}。在这里我们为了说明问题的简便性，我们假定P(x){P(x)}为由两个高斯分布混合得到的高斯混合模型，而Q(x){Q(x)}为高斯分布，两种KL散度定义为：

DKL(p∣∣q)=Ex∼P[log⁡P(x)−log⁡Q(x)]{ D_{KL}(p \vert \vert q) = \mathbb{E}_{x\sim P} \left[ \log P(x) - \log Q(x) \right] }

DKL(q∣∣p)=Ex∼Q[log⁡Q(x)−log⁡P(x)]{ D_{KL}(q \vert \vert p) = \mathbb{E}_{x\sim Q} \left[ \log Q(x) - \log P(x) \right] }

KL散度描述了在已知的分布上，函数log⁡P(x)−log⁡Q(x){\log P(x) - \log Q(x)}的期望。已知的高斯混合分布模型具有两个峰，优化KL散度，Q(x){Q(x)}只有单峰，它就必须要在这两个峰上的值偏小，并且还要保证中间的单峰和P(x){P(x)}偏差不会太大，所以它会模糊地将多个峰聚合在一起，并且贴合P(x){P(x)}，也就是单个高斯分布的σ2{\sigma^{2}}会偏大。

而逆KL散度描述了在未知的分布上，函数log⁡Q(x)−log⁡P(x){\log Q(x) - \log P(x)}的期望。Q(x){Q(x)}仅有单峰，它必须贴合某个峰，而在另外一个峰的值足够的小（这样它在另一个峰的期望会很小），所以它会选择单个峰，并且使得σ2{\sigma^{2}}偏小。

下面我们将从理论和数值实验上对KL散度的非对称性做进一步的说明。

理论说明

假设混合高斯分布模型由两个单高斯条件分布按概率p1,p2{p_{1},p_{2}}混合而成

两个单高斯条件分布为：

X1∼N(μ1,σ12){ X_{1} \sim \mathcal{N}(\mu_{1}, \sigma_{1}^{2}) }

X2∼N(μ2,σ22){X_{2} \sim \mathcal{N}(\mu_{2}, \sigma_{2}^{2}) }

假设它们的概率密度函数分别为p1(x){p_{1}(x)}和p2(x){p_{2}(x)}，则混合高斯模型的概率密度函数可以表示为：

p(x)=p1p1(x)+p2p2(x){p(x) = p_{1}p_{1}(x) + p_{2}p_{2}(x) }

该混合高斯模型是给定的，参数p1,p2,μ1,μ2,σ12,σ22{p_{1},p_{2},\mu_{1},\mu_{2},\sigma_{1}^{2},\sigma_{2}^{2}}都是已知的
常数。

现在使用单高斯分布模型来近似p(x){p(x)}，假设它的均值和方差为μ{\mu}和σ2{\sigma^{2}}，它的
概率密度函数为：

q(x)=12πσe(−(x−μ)22σ2){ q(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{\left(- \frac{(x-\mu)^{2}}{2\sigma^{2}}\right)} }

KL散度的情况下

(1) 在第一种KL散度DKL(p∣∣q){D_{KL}\left(p \vert \vert q\right)}作为衡量单高斯分布模型拟合
混合高斯分布模型的近似程度的的情况下。

DKL(p∣∣q)=Ex∼p[log⁡p(x)−log⁡q(x)]=∫[log⁡p(x)−log⁡q(x)]p(x)dx=∫[log⁡p(x)]p(x)dx−∫[log⁡q(x)]p(x)dx{ \begin{aligned} D_{KL}(p \vert \vert q) &= \mathbb{E}_{x \sim p} \left[ \log p(x) - \log q(x) \right] \\ &= \int \left[ \log p(x) - \log q(x) \right] p(x) dx \\ &= \int \left[ \log p(x) \right] p(x) dx - \int \left[ \log q(x) \right] p(x) dx \\ \end{aligned} }

上式的左项为常数，要使得DKL{D_{KL}}最小，右项要取得最大值，令右项为L{L}。

L=∫[log⁡q(x)]p(x)dx=∫log⁡(12πσe(−(x−μ)22σ2))p(x)dx=∫(−log⁡2π−log⁡σ−12σ2(x−μ)2)p(x)dx=−log⁡2π−log⁡σ−12σ2∫(x−μ)2p(x)dx{ \begin{aligned} L &= \int \left[ \log q(x) \right] p(x) dx \\ &= \int \log \left( \frac{1}{\sqrt{2 \pi} \sigma} e^{\left(- \frac{(x-\mu)^{2}}{2\sigma^{2}}\right)} \right) p(x) dx \\ &= \int \left( -\log \sqrt{2 \pi} - \log \sigma - \frac{1}{2\sigma^{2}} (x-\mu)^{2} \right) p(x) dx \\ &= -\log \sqrt{2 \pi} - \log \sigma - \frac{1}{2\sigma^{2}} \int (x - \mu)^{2} p(x) dx \\ \end{aligned} }

令T=∫(x−μ)2p(x)dx{T = \int (x - \mu)^{2} p(x) dx}，L{L}要取得最大值，T{T}要取得最小值。

T=∫(x2−2μx+μ2)p(x)dx=∫x2p(x)dx−2μ∫xp(x)dx+μ2∫p(x)dx{ \begin{aligned} T &= \int \left( x^{2} - 2\mu x + \mu^{2} \right) p(x) dx \\ &= \int x^{2} p(x) dx - 2\mu \int x p(x) dx + \mu^{2} \int p(x) dx \\ \end{aligned} }

则L{L}对μ{\mu}的导数为：

∂L∂μ=∂L∂T∂T∂μ=−12σ2(2μ−2∫xp(x)dx)=0{ \begin{aligned} \frac{\partial L}{\partial \mu} &= \frac{\partial L}{\partial T} \frac{\partial T}{\partial \mu} \\ &= -\frac{1}{2\sigma^{2}}\left(2\mu - 2\int x p(x)dx \right) = 0 \end{aligned} }

求得最优解μ0{\mu_0}:

μ0=∫xp(x)dx=p1∫xp1(x)dx+p2∫xp2(x)dx=p1μ1+p2μ2{ \mu_{0} = \int x p(x) dx = p_{1} \int x p_{1}(x) dx + p_{2} \int x p_{2}(x) dx = p_{1}\mu_{1} + p_{2}\mu_{2} }

此时T{T}取得最小值，

而L{L}对σ{\sigma}的导数为：

∂L∂σ=−1σ+Tσ3=1σ(Tσ2−1)=0{ \begin{aligned} \frac{\partial L}{\partial \sigma} &= - \frac{1}{\sigma} + \frac{T}{\sigma^{3}} \\ &= \frac{1}{\sigma} \left( \frac{T}{\sigma^{2}} - 1 \right) = 0 \end{aligned} }

得最优解σ0{\sigma_{0}}：

σ02=T=p1∫x2p1(x)dx+p2∫x2p2(x)dx−2μ02+μ02=p1(σ12+μ12)+p2(σ22+μ22)−(p1μ1+p2μ2)2{ \begin{aligned} \sigma_{0}^{2} &= T \\ &= p_{1} \int x^{2} p_{1}(x)dx + p_{2} \int x^{2} p_{2}(x) dx - 2 \mu_{0}^{2} + \mu_{0}^{2} \\ &= p_{1} (\sigma_{1}^{2} + \mu_{1}^{2}) + p_{2}(\sigma_{2}^{2} + \mu_{2}^{2}) - (p_{1}\mu_{1} + p_{2}\mu_{2})^{2} \end{aligned} }

可以看到当取得最优解的时候，μ0{\mu_{0}}是混合高斯模型的两个条件分布模型的均值的期望，而且
μ1≤μ0=p1μ1+p2μ2≤μ2{ \mu_{1} \leq \mu_{0} = p_{1}\mu_{1} + p_{2}\mu_{2} \leq \mu_{2} }，说明此时的最佳
拟合的单高斯分布选择是将混合高斯模型的多个峰值聚合起来。

逆KL散度情况下

(2) 在第二种KL散度DKL(q∣∣p){D_{KL}(q \vert \vert p)}作为衡量单高斯分布模型拟合混合高
斯分布模型的近似程度的的情况下。

DKL(q∣∣p)=Ex∼q[log⁡q(x)−log⁡p(x)]=∫[log⁡q(x)−log⁡p(x)]q(x)dx=∫(log⁡q(x))q(x)dx−∫(log⁡p(x))q(x)dx{ \begin{aligned} D_{KL}(q\vert \vert p) &= \mathbb{E}_{x \sim q}\left[ \log q(x) - \log p(x) \right] \\ &= \int \left[ \log q(x) - \log p(x) \right] q(x) dx \\ &= \int \left( \log q(x) \right) q(x) dx - \int \left( \log p(x) \right) q(x) dx \\ \end{aligned} }

令A=∫(log⁡q(x))q(x)dx{A = \int \left( \log q(x) \right) q(x) dx}，B=∫(log⁡p(x))q(x)dx{B = \int \left( \log p(x) \right) q(x) dx }，要使得
DKL(q∣∣p){D_{KL}(q \vert \vert p)}取得最小值，A{A}要取得最大值，B{B}要取得最小值。

A=∫(log⁡q(x))q(x)dx=∫−log⁡2π−log⁡σ−(x−μ)22σ2q(x)dx=−log⁡2π−log⁡σ−12σ2∫(x−μ)2q(x)dx=−log⁡2π−log⁡σ−12{ \begin{aligned} A &= \int \left( \log q(x) \right) q(x) dx \\ &= \int - \log \sqrt{2\pi} -\log \sigma - \frac{(x-\mu)^{2}}{2\sigma^{2}} q(x) dx \\ &= -\log \sqrt{2\pi} - \log \sigma - \frac{1}{2\sigma^{2}} \int (x-\mu)^{2} q(x) dx \\ &= -\log \sqrt{2\pi} - \log \sigma - \frac{1}{2} \end{aligned} }

可以看到A{A}的取值和μ{\mu}无关。

B=∫(log⁡p(x))q(x)dx=∫log⁡[p1p1(x)+p2p2(x)]q(x)dx=∫log⁡[p1p1(x)]q(x)dx+∫log⁡[1+p2p2(x)p1p1(x)]q(x)dx{ \begin{aligned} B &= \int (\log p(x))q(x) dx \\ &= \int \log \left[ p_{1}p_{1}(x) + p_{2}p_{2}(x) \right] q(x) dx \\ &= \int \log \left[ p_{1}p_{1}(x) \right] q(x) dx + \int \log \left[ 1 + \frac{p_{2}p_{2}(x)}{p_{1}p_{1}(x)} \right] q(x) dx \\ \end{aligned} }

令B1=∫log⁡[p1p1(x)]q(x)dx{B_{1} = \int \log \left[ p_{1}p_{1}(x) \right] q(x) dx }，B2=∫log⁡[1+p2p2(x)p1p1(x)]q(x)dx{B_{2} = \int \log \left[ 1 + \frac{p_{2}p_{2}(x)}{p_{1}p_{1}(x)} \right] q(x) dx}

B1=log⁡p1+∫[log⁡p1(x)]q(x)dx=log⁡p1−log⁡((2π))−log⁡σ1−12σ12∫(x−μ1)2q(x)dx=log⁡p1−log⁡((2π))−log⁡σ1−12σ12(μ2+σ2−2μ1μ+μ12){ \begin{aligned} B_{1} &= \log p_{1} + \int \left[ \log p_{1}(x) \right] q(x) dx \\ &= \log p_{1} - \log\left( \sqrt(2\pi)\right) - \log \sigma_{1} - \frac{1}{2\sigma_{1}^{2}} \int (x - \mu_{1})^{2} q(x) dx\\ &= \log p_{1} - \log\left( \sqrt(2\pi)\right) - \log \sigma_{1} - \frac{1}{2\sigma_{1}^{2}} \left( \mu^{2} + \sigma^{2} -2\mu_{1}\mu + \mu_{1}^{2} \right) \end{aligned} }

B1{B_{1}}是关于μ{\mu}的二次函数，当μ=μ1{\mu = \mu_{1}}时，B1{B_{1}}取得最大值。

B2=∫log⁡[1+p2p2(x)p1p1(x)]q(x)dx<∫p2p2(x)p1p1(x)q(x)dx=p2p1∫1σ2e−(x−μ2)22σ221σ1e−(x−μ1)22σ1212πσe−(x−μ)22σ2dx=p2σ1p1σ212πσ1∫e(x−μ1)22σ12−(x−μ2)22σ22−(x−μ)22σ2dx{ \begin{aligned} B_{2} &= \int \log \left[ 1 + \frac{p_{2}p_{2}(x)}{p_{1}p_{1}(x)} \right] q(x) dx \\ &< \int{\frac{p_{2}p_{2}(x)}{p_{1}p_{1}(x)} q(x) dx} \\ &= \frac{p_{2}}{p_{1}} \int \frac{ \frac{1}{\sigma_{2}} e^{-\frac{(x - \mu_{2})^{2}}{2\sigma_{2}^{2}}} }{ \frac{1}{\sigma_{1}} e^{-\frac{(x-\mu_{1})^{2}}{2\sigma_{1}^{2}}} } \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &= \frac{p_{2}\sigma_{1}}{p_{1}\sigma_{2}} \frac{1}{\sqrt{2\pi}\sigma_{1}} \int e^{\frac{(x-\mu_{1})^{2}}{2\sigma_{1}^{2}} - \frac{(x-\mu_{2})^{2}}{2\sigma_{2}^{2}} - \frac{(x-\mu)^{2}}{2\sigma^{2}} } dx \\ \end{aligned} }

如果我们取使得B1{B_{1}}为最大值的μ=μ1{\mu = \mu_{1}}，并使得σ=σ1{\sigma = \sigma_{1}}，此时

B2<p2σ1p1σ212πσ1∫e−(x−μ2)22σ22=p2σ1p1σ212πσ12πσ2∫p2(x)dx=p2p1{ \begin{aligned} B_{2} &< \frac{p_{2}\sigma_{1}}{p_{1}\sigma_{2}} \frac{1}{\sqrt{2\pi}\sigma_{1}} \int e^{- \frac{(x-\mu_{2})^{2}}{2\sigma_{2}^{2}}} \\ &= \frac{p_{2}\sigma_{1}}{p_{1}\sigma_{2}} \frac{1}{\sqrt{2\pi}\sigma_{1}} \sqrt{2\pi}\sigma_{2} \int p_{2}(x) dx \\ &= \frac{p_{2}}{p_{1}} \\ \end{aligned} }

即此时有B2<p2p1{B_{2} < \frac{p_{2}}{p_{1}}}，如果p2≪p1{p_{2} \ll p_{1}}，那么B2{B_{2}}接近于0，我们就可以忽略该项，那
我们选取μ=μ1{\mu = \mu_{1}}就是最优值。

同理如果我们在得到B{B}推导的最后一步，将B{B}拆解为：

B=∫log⁡[p2p2(x)]q(x)dx+∫log⁡[1+p1p1(x)p2p2(x)]q(x)dx=B1′+B2′{ \begin{aligned} B &= \int \log \left[ p_{2}p_{2}(x) \right] q(x) dx + \int \log \left[ 1 + \frac{p_{1}p_{1}(x)}{p_{2}p_{2}(x)} \right] q(x) dx \\ &= B_{1}' + B_{2}' \end{aligned} }

我们可以得到，当p1≪p2{p_{1} \ll p_{2}}时，我们选取μ=μ2{\mu = \mu_{2}}就是最优解。

而这两种拆分的方式只是依据p1,p2{p_{1},p_{2}}的大小而定，它们是等价的，我们假定当p2<p1{p_{2} < p_{1}}时使用第一种拆分方式，
当p1<p2{p_{1} < p_{2}}时使用第二种拆分方式，并令它们的比值为k{k}，那么当p1=p2{p_{1} = p_{2}}时，k{k}取得最大值为1。
也就是说B2≤1{B_{2} \le 1}，它总是可忽略的。

综上所述，使用第二种KL散度作为作为衡量单高斯分布模型拟合混合高斯分布模型的近似程度的情况下，单个高斯分布模型会倾向于偏向p{p}更大的混合概率模型中的单峰。

计算实验

我们使用数值模拟的方法求解给定的混合高斯模型的单个高斯模型近似的μ{\mu}和σ2{\sigma^{2}}的最优解。

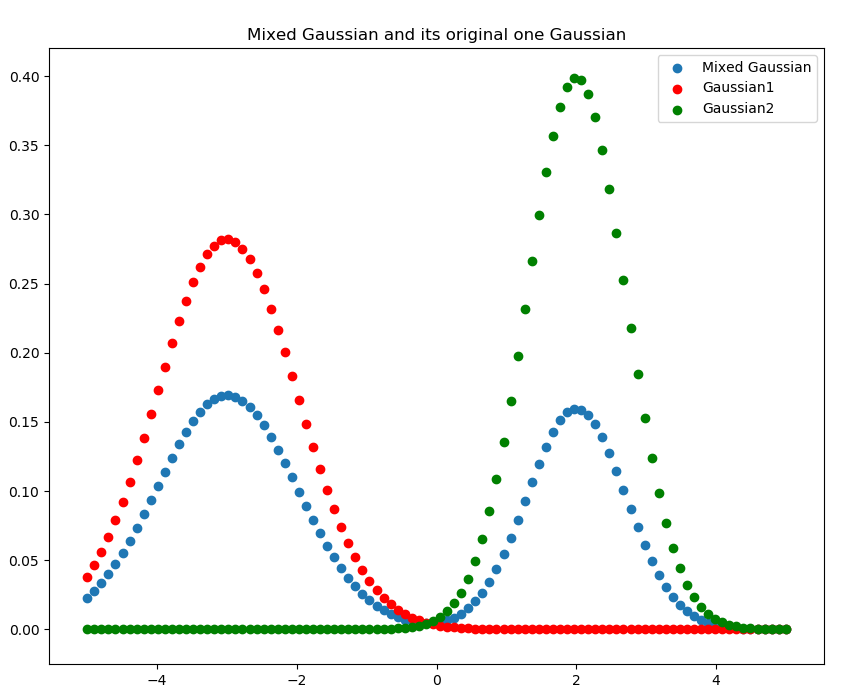
给定混合高斯模型X=p1X1+p2X2{X = p_{1}X_{1} + p_{2}X_{2}}。

其中p1=0.6,p2=0.4,X1∼N(−3,2),X2∼N(2,1){p_{1} = 0.6, p_{2} = 0.4, X_{1} \sim \mathcal{N}(-3, 2), X_{2} \sim \mathcal{N}(2,1)}

概率密度函数如下图所示。

混合高斯模型概率密度函数图像
混合高斯模型概率密度函数图像

KL散度情况下

使用KL散度作为衡量单高斯分布模型拟合混合高斯分布模型的近似程度的情况下

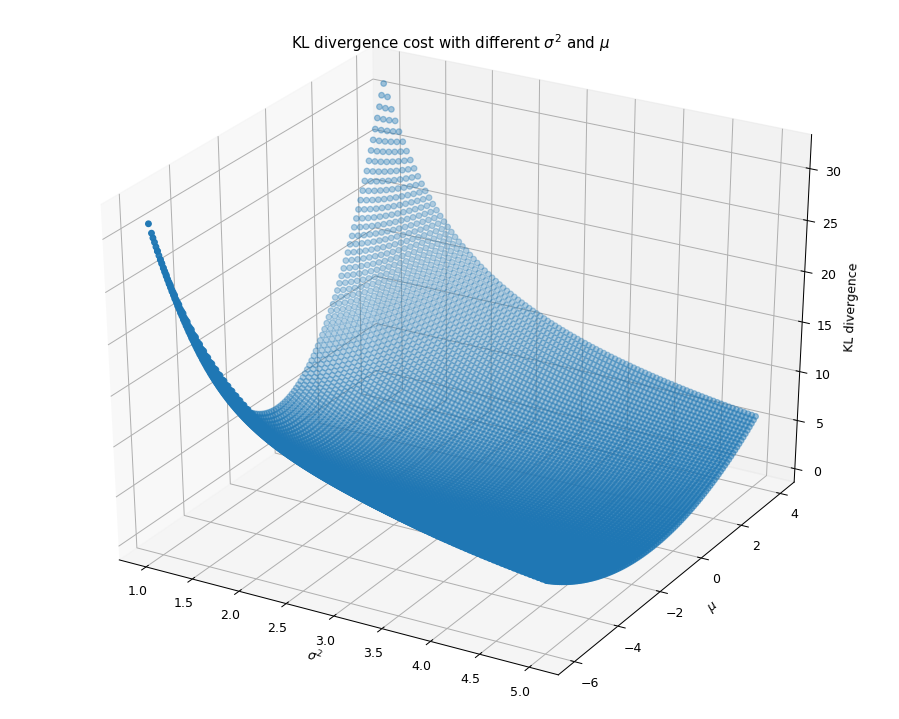
下图给出了KL散度和不同σ2,μ{\sigma^{2},\mu}取值的二元函数的图像，
我们发现该二元函数比较平滑。

KL散度和不同${sigma^{2},mu}$取值的二元函数的图像
KL散度和不同${sigma^{2},mu}$取值的二元函数的图像

给定初始值μ=1,σ2=1{\mu=1,\sigma^{2}=1}使用梯度下降公式迭代求得

最优解为：μ=−0.99966166,σ2=6.45287537{\mu = -0.99966166, \sigma^{2} = 6.45287537}。
这与我们计算得到的μ=p1μ1+p2μ2{\mu = p_{1}\mu_{1} + p_{2}\mu_{2}}的公式吻合。

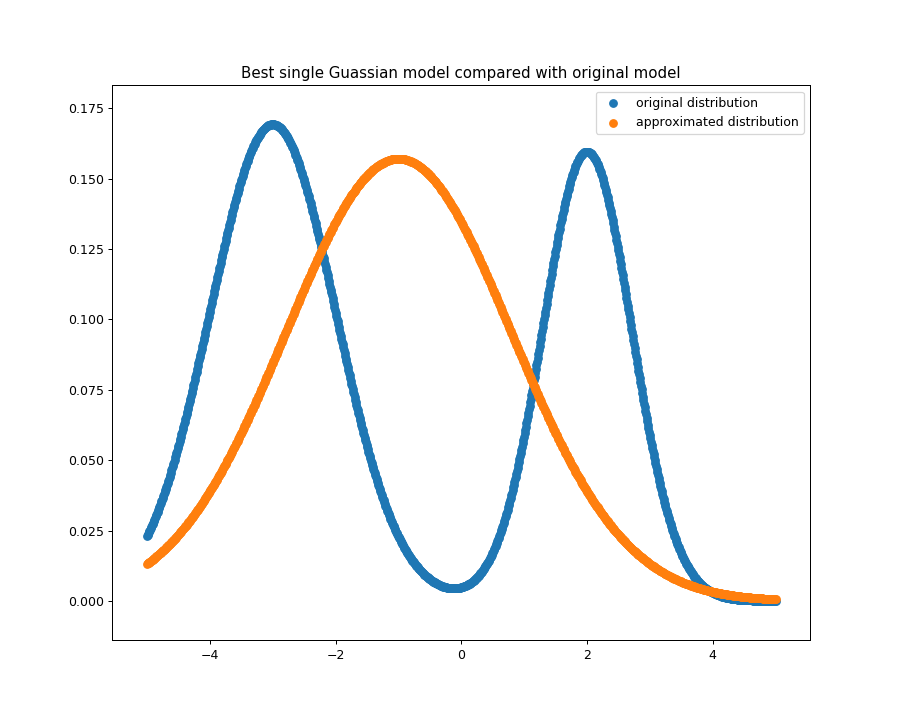
我们画出得到的最佳的高斯分布的图像如下图所示，单个的高斯分布模型模糊地将
混合高斯模型的几个峰模糊地聚合了起来。

KL散度下最佳单个高斯分布模型
KL散度下最佳单个高斯分布模型

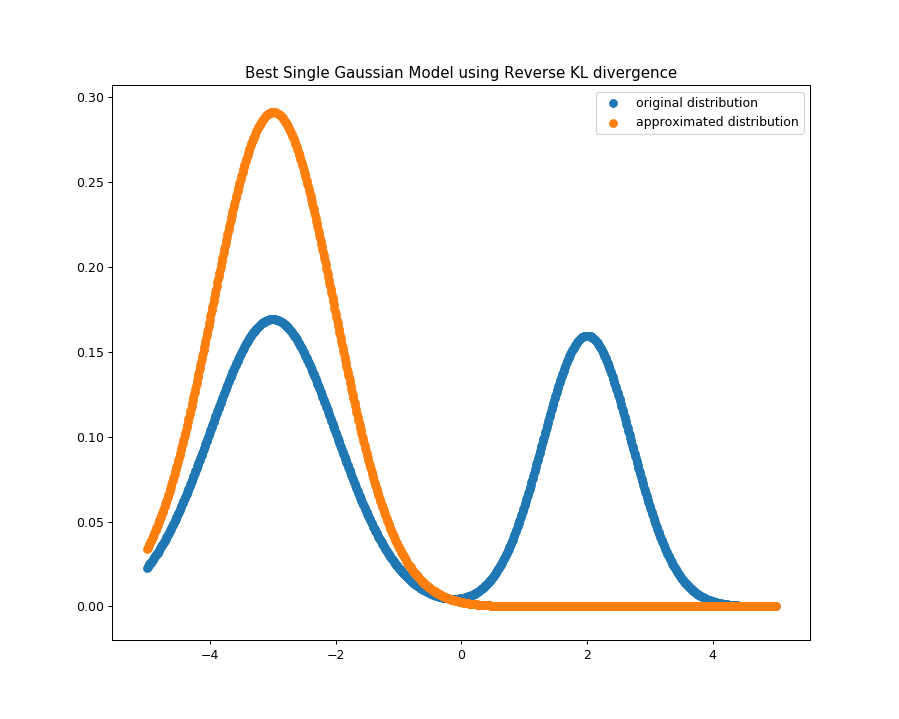
逆KL散度情况下

使用逆KL散度作为衡量单高斯分布模型拟合混合高斯分布模型的近似程度的的情况下

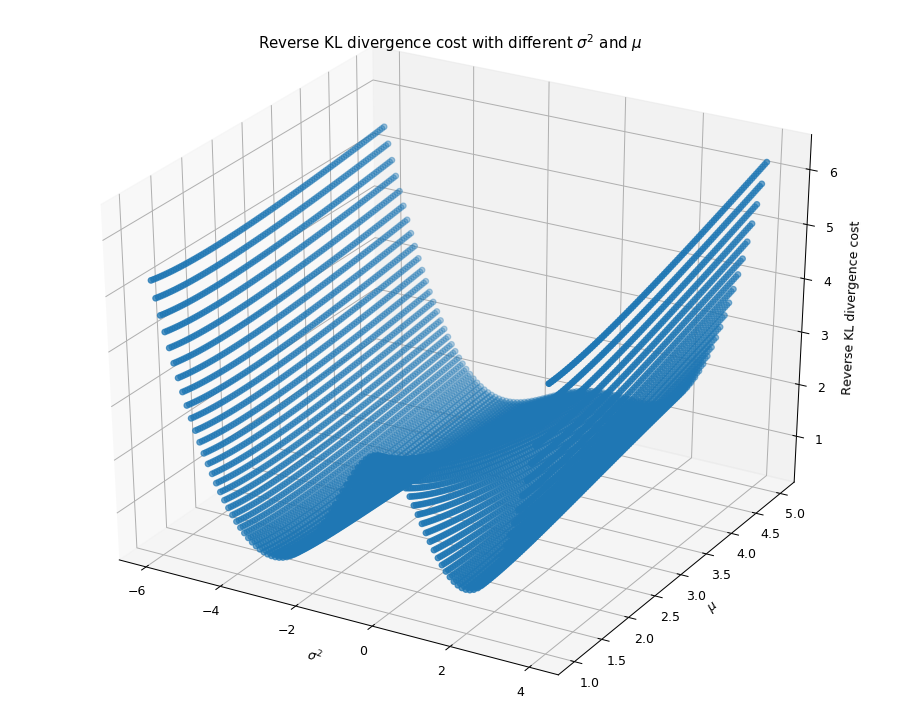
下图给出了逆KL散度和不同σ2,μ{\sigma^{2},\mu}取值的二元函数的图像，
同样的我们发现该二元函数也比较平滑。

KL散度与不同的${sigma^{2}}$和${mu}$取值的关系
KL散度与不同的${sigma^{2}}$和${mu}$取值的关系

给定初始值μ=−1,σ2=1{\mu=-1,\sigma^{2}=1}使用梯度下降公式迭代求得

最优解为：μ=−2.98863212,σ2=1.87676299{\mu = -2.98863212, \sigma^{2} = 1.87676299}，这也与我们理论推导的结论相吻合。

此时得到的单个高斯分布模型的图像如下图所示，我们看到该高斯分布会选择概率比较大的峰拟合。

逆KL散度下最佳的单个高斯分布模型
逆KL散度下最佳的单个高斯分布模型

实验的代码将发布在我的github上。

实验细节：

  • 使用Simpson公式计算KL散度中连续性变量的期望的积分，而且在我们给定的高斯分布下，处于区间[−20,20]{[-20,20]}之外的值的概率密度是非常小的，所以我们将积分的上下限替换为20和-20，而不是正负无穷。
  • 我们使用梯度下降法求解最优的参数。
  • 在梯度下降法中，我们使用中心差商公式来求得梯度，虽然使用数值方法计算梯度的做法非常不好，但是本次实验中两种KL散度的cost函数比较光滑，所以数值计算的结果也可以比较精确。