本文主要讨论用于衡量图片质量的常用方法和用于评估 GAN 效果的方法。
MSEPSNRSSIM[1]MS-SSIM[2]
方法主要是衡量两张图片的相似度,以下用X {X} X Y {Y} Y X {X} X Y {Y} Y Y {Y} Y
MSE
就是两张图片的像素差的平方的均值。
M S E ( X , Y ) = 1 M N ∑ i = 1 M ∑ j = 1 N ( X i , j − Y i , j ) 2 {
MSE(X,Y) = \frac{1}{MN} \sum_{i = 1}^{M} \sum_{j = 1}^{N} (X_{i,j} - Y_{i,j})^{2}
} M S E ( X , Y ) = M N 1 i = 1 ∑ M j = 1 ∑ N ( X i , j − Y i , j ) 2
容易知道,MSE 是越小,两张图片越接近,质量也就越好 。 RMSE 就是再开个根号。
PSNR(Peak Singal-to-noise ratio) 峰值信噪比
最高响应(可以取得的最大值,对8bit图片就是255)的平方除以MSE,再取对数。
P S N R ( X , Y ) = 10 log 10 ( M A X 2 M S E ( X , Y ) ) {
PSNR(X,Y) = 10 \log_{10} \left( \frac{MAX^{2}}{MSE(X,Y)} \right)
} P S N R ( X , Y ) = 1 0 log 1 0 ( M S E ( X , Y ) M A X 2 )
PSNR 是越大越好 ,但是没有上界。
SSIM 分三个部分:
亮度:l ( X , Y ) {l(X,Y)} l ( X , Y )
对比度:c ( X , Y ) {c(X,Y)} c ( X , Y )
结构相似度:s ( X , Y ) {s(X,Y)} s ( X , Y )
S S I M ( X , Y ) = [ l ( X , Y ) ] α [ c ( X , Y ) ] β [ s ( X , Y ) ] γ {
SSIM(X,Y) = [l(X,Y)]^{\alpha} [c(X,Y)]^{\beta} [s(X,Y)]^{\gamma}
} S S I M ( X , Y ) = [ l ( X , Y ) ] α [ c ( X , Y ) ] β [ s ( X , Y ) ] γ
l ( x , y ) = 2 μ x μ y + C 1 u x 2 + u y 2 + C 1 c ( x , y ) = 2 σ x σ y + C 2 σ x 2 + σ y 2 + C 2 s ( x , y ) = σ x , y + C 3 σ x σ y + C 3 {
\begin{aligned}
l(\mathbf{x},\mathbf{y}) &= \frac{2 \mu_{x} \mu_{y} + C_{1}}{u_{x}^{2} + u_{y}^{2} + C_{1}} \\
c(\mathbf{x},\mathbf{y}) &= \frac{2 \sigma_{x} \sigma_{y} + C_{2}}{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2}} \\
s(\mathbf{x},\mathbf{y}) &= \frac{\sigma_{x,y} + C_{3}}{\sigma_{x}\sigma_{y} + C_{3}}
\end{aligned}
} l ( x , y ) c ( x , y ) s ( x , y ) = u x 2 + u y 2 + C 1 2 μ x μ y + C 1 = σ x 2 + σ y 2 + C 2 2 σ x σ y + C 2 = σ x σ y + C 3 σ x , y + C 3
其中μ x , μ y , σ x 2 , σ y 2 , σ x , y {\mu_{x},\mu_{y},\sigma_{x}^{2},\sigma_{y}^{2},\sigma_{x,y}} μ x , μ y , σ x 2 , σ y 2 , σ x , y x , y {x,y} x , y
上述的SSIM计算公式包含的超参数有:三种指标的比例α , β , γ {\alpha, \beta, \gamma} α , β , γ C 1 , C 2 , C 3 {C_{1},C_{2},C_{3}} C 1 , C 2 , C 3
在实际的SSIM计算中一般会将上面的式子进行变换:取α = β = γ = 1 {\alpha = \beta = \gamma = 1} α = β = γ = 1 C 3 = C 2 / 2 {C_{3} = C_{2} / 2} C 3 = C 2 / 2 ,式子变为:
S S I M ( x , y ) = ( 2 μ x μ y + C 1 ) ( 2 σ x , y + C 2 ) ( μ x 2 + μ y 2 + C 1 ) ( σ x 2 + σ y 2 + C 2 ) = l ( x , y ) 2 σ x , y + C 2 σ x 2 + σ y 2 + C 2 {
\begin{aligned}
SSIM(\mathbf{x},\mathbf{y}) &= \frac{(2 \mu_{x} \mu_{y} + C_{1})(2 \sigma_{x,y} + C_{2})}{(\mu_{x}^{2} + \mu_{y}^{2} + C_{1})(\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2})} \\
&= l(\mathbf{x},\mathbf{y}) \frac{2 \sigma_{x,y} + C_{2}}{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2}}
\end{aligned}
} S S I M ( x , y ) = ( μ x 2 + μ y 2 + C 1 ) ( σ x 2 + σ y 2 + C 2 ) ( 2 μ x μ y + C 1 ) ( 2 σ x , y + C 2 ) = l ( x , y ) σ x 2 + σ y 2 + C 2 2 σ x , y + C 2
而且使用 NxN 的窗口,窗口按照类似滤波器的方式在图片上以strid=1移动,每次计算窗口内的局部SSIM,最后取平均值 。
可以借助已有的卷积函数(如pytorch的torch.nn.functional.conv2d),只要设置卷积核为box filter,就可以求得各个window的均值 ,再借助方差、协方差的公式:
σ X 2 = E X 2 − ( E X ) 2 {
\sigma_{X}^{2} = \mathbb{E}X^{2} - (\mathbb{E}X)^{2}
} σ X 2 = E X 2 − ( E X ) 2
σ X , Y = E ( X Y ) − E X E Y {
\sigma_{X,Y} = \mathbb{E}(XY) - \mathbb{E}X\mathbb{E}Y
} σ X , Y = E ( X Y ) − E X E Y
这样计算起来比较高效。
但是在官方实现的matlab代码中默认使用的是大小为11x11,σ = 1.5 {\sigma = 1.5} σ = 1 . 5 。所以在一份pytorch的实现(见下面)中也是用的高斯滤波器。
C 1 , C 2 {C_{1},C_{2}} C 1 , C 2
C i = ( K i L ) 2 ( i = 1 , 2 ) {
C_{i} = (K_{i} L)^{2} \qquad (i = 1, 2)
} C i = ( K i L ) 2 ( i = 1 , 2 )
其中 L {L} L K 1 , K 2 {K_{1},K_{2}} K 1 , K 2 ( 0.01 , 0.03 ) {(0.01,0.03)} ( 0 . 0 1 , 0 . 0 3 )
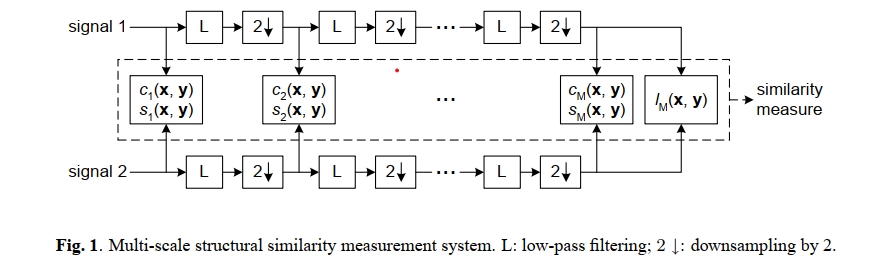
MS-SSIM 在 SSIM 的基础上扩展成多个尺度的,idea是人眼对中间频率最敏感(human visual sensitivity peaks at middle frequencies (around 4 cycles per degree of visual angle) and decreases along both high- and low-frequency directions[2])。
对原图,进行低通滤波、下采样(大小减半)得到每一个scale的图片,共进行M − 1 {M - 1} M − 1
除了最底层的scale ,对第j = 0 , ⋯ , M − 1 {j = 0,\cdots,M-1} j = 0 , ⋯ , M − 1 c j ( x , y ) , s j ( x , y ) {c_{j}(\mathbf{x},\mathbf{y}),s_{j}(\mathbf{x},\mathbf{y})} c j ( x , y ) , s j ( x , y )
最底层的scale,三种指标都计算 ,记作l M ( x , y ) , c M ( x , y ) , s M ( x , y ) {l_{M}(\mathbf{x},\mathbf{y}),c_{M}(\mathbf{x},\mathbf{y}),s_{M}(\mathbf{x},\mathbf{y})} l M ( x , y ) , c M ( x , y ) , s M ( x , y )
最后按照下式计算它们的乘积:
M S S S I M ( x , y ) = [ l M ( x , y ) ] α M ∏ j = 1 M [ c j ( x , y ) ] β j [ s j ( x , y ) ] γ j {
MSSSIM(\mathbf{x},\mathbf{y}) = [l_{M}(\mathbf{x},\mathbf{y})]^{\alpha_{M}} \prod_{j = 1}^{M} [c_{j}(\mathbf{x},\mathbf{y})]^{\beta_{j}} [s_{j}(\mathbf{x},\mathbf{y})]^{\gamma_{j}}
} M S S S I M ( x , y ) = [ l M ( x , y ) ] α M j = 1 ∏ M [ c j ( x , y ) ] β j [ s j ( x , y ) ] γ j
如下图所示:
MS-SSIM计算方式
一般:
取M {M} M
且对每个scale的α j = β j = γ j {\alpha_{j} = \beta_{j} = \gamma_{j}} α j = β j = γ j
对所有的j,保证∑ j = 1 M γ j = 1 {\sum_{j = 1}^{M} \gamma_{j} = 1} ∑ j = 1 M γ j = 1
如果接着令C 3 = C 2 / 2 {C_{3} = C_{2} / 2} C 3 = C 2 / 2
M S S S I M ( x , y ) = [ l M ( x , y ) ] γ M ∏ j = 1 M [ 2 σ x , y , j + C 2 σ x , j 2 + σ y , j 2 + C 2 ] γ j {
MSSSIM(\mathbf{x},\mathbf{y}) = [l_{M}(\mathbf{x},\mathbf{y})]^{\gamma_{M}} \prod_{j = 1}^{M} [\frac{2 \sigma_{x,y,j} + C_{2}}{\sigma_{x,j}^{2} + \sigma_{y,j}^{2} + C_{2} }]^{\gamma_{j}}
} M S S S I M ( x , y ) = [ l M ( x , y ) ] γ M j = 1 ∏ M [ σ x , j 2 + σ y , j 2 + C 2 2 σ x , y , j + C 2 ] γ j
数值问题:
和之前SSIM说的一样,MS-SSIM 的计算中的协方差可能为负数,对负数取分数指数,会导致nan ,通常的做法是:
调大C 2 {C_{2}} C 2 。将协方差所有负数值置0,relu 。
超参数取值:
文章[2]中,作者对M = 5 {M=5} M = 5 γ i {\gamma_{i}} γ i ( 0.0448 , 0.2856 , 0.3001 , 0.2363 , 0.1333 ) {(0.0448,0.2856,0.3001,0.2363,0.1333)} ( 0 . 0 4 4 8 , 0 . 2 8 5 6 , 0 . 3 0 0 1 , 0 . 2 3 6 3 , 0 . 1 3 3 3 )
SSIM, MS-SSIM 可以用于衡量两张图片的相似性,ACGAN[4] 将它引入,用于衡量各类别生成的图片的多样性,和检测训练中的mode collapse问题 。
具体的做法其实很简单:
对每个类别生成的图片,任意选择100对,衡量两两的 MS-SSIM,取均值 ,得分高表明该类生成的图像都非常相似,所以图片的多样性比较低,反之图片的多样性高 。
SSIM 主页 (包含一份 matlab 代码)SSIM,MS-SSIM pytorch 实现 我的实现
Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600–612. https://doi.org/10.1109/TIP.2003.819861
Wang, Z., Simoncelli, E. P., & Bovik, A. C. (2003). Multi-scale structural similarity for image quality assessment . Conference Record of the Asilomar Conference on Signals, Systems and Computers, 2, 1398–1402. https://doi.org/10.1109/acssc.2003.1292216
结构相似性 wikipedia
Odena, A., Olah, C., & Shlens, J. (2017). Conditional image synthesis with auxiliary classifier gans. 34th International Conference on Machine Learning, ICML 2017, 6, 4043–4055.