Introduction
本文是对几篇GAN的略读,主要阐述想法和技术,其中蕴含的idea或者实现细节搁置不提,有机会再提出来单独讲讲吧,included papers:
SGAN (Stacked GAN)
SGAN属于Conditional GAN的一种(文章指出进行修改也可以进行unsupervised学习),在模型上采用了多层级的G和D的架构,并使用一个预训练的分类DNN,它将多层级的G的目标看成是invert DNN的forward的过程,抽出它的不同层级的特征作为不同层级的GAN的目标,希望不同层级的GAN学习到DNN输出的高层特征到DNN输入的底层特征的解码。
同时SGAN还有分层单独训练和端到端的两种训练方法。
模型
模型主要包括三个部分:
- 用于分类的pre-trained DNN,把预训练的分类网络划分成不同的blocks(conv + pooling的组合),称之为Encoder:Ei。
- 用于invert某一层Ei的生成器:Gi
- Gi对应的Di,用于计算GAN Loss。
Encoders
每一个Ei的输入hi是上一层的输出: h0为训练的图片,hN为标签。
hi+1=Ei(hi)
Generators
Gi接受Ei的输出和噪声:
hi^=Gi(hi+1,z)
当使用端到端的训练时,Gi接受上一层生成器的输出:
hi^=Gi(hi+1^,z)
进一步,作者解释了使用多层的生成器的idea:将label到image的条件分布变成了多个分布的联合分布,而每个Gi对中间的简单的分布进行建模:
PG(x^∣y)=PG(h0^∣hN^)∝PG(h0^,⋯,hN−1^∣hN^)=i∏PGi(hi^∣hi+1^)
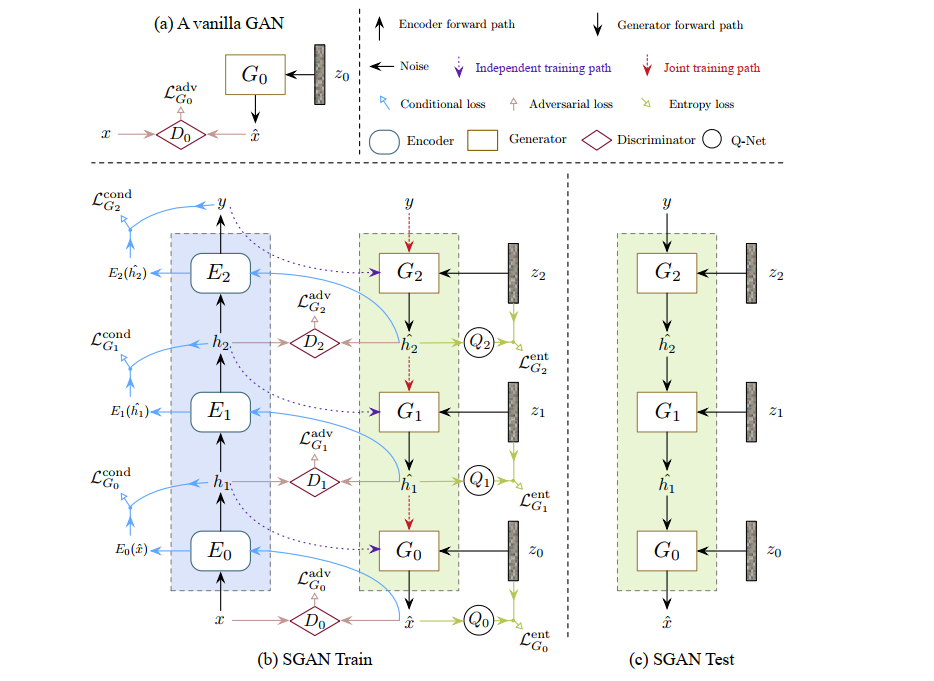
整体模型架构
Loss
每层的GAN采用了三种Loss训练:
LGi=λ1LGiadv+λ2LGicond+λ3LGient
GAN Loss
GAN Loss使用的原始paper中提到的修改过的Vanilla GAN Loss,每个层级的Di需要鉴别该层级的真实的图片输入的featurehi和Gi生成的featurehi^的真实性。
Di∗=max[Ehi[logDi(hi)]+Ehi+1,z[log(1−Di(Gi(hi+1,z)))]]
Gi∗=maxEhi+1,z[log(Di(Gi(hi+1,z)))]
Conditional Loss
Idea是防止Gi忽略conditional的信息hi+1,在某种意义上可以看成是重建的Loss。
具体做法是将hi^再带入到Ei中得到hi+1′,优化它和hi+1的差异。
LGicond=Ehi+1,z[f(Ei(Gi(hi+1,z)),hi+1)]
Entropy Loss
使用conditional loss的同时,GAN又可能会忽略噪声z的影响,所以这一项是为了防止忽略噪声,我觉得可以把conditional loss看成重建误差,目的是提高图片质量,而这里的误差可以看成是为了提高生成图片的多样性,所以也很像一个图像质量和多样性的trade-off。
作者首先提到现有(当时)的方法没有很好地解决这一问题,接着从信息熵的角度提出了和InfoGAN类似的方法。
LGient=Ezi[Ehi^[−logQi(zi∣hi^)]]
为了鼓励diversity,转化成提高Gi的建模的分布p(hi^∣hi+1)的熵:H(hi^∣hi+1),作者用Variational Conditional Entropy Maximization 的方法证明了优化上式的Entropy Loss是提高熵(证明不详述,和InfoGAN中的证明非常类似)。
思想也是用一个Qi分布去近似后验分布Pi(z∣hi^),实际中Qi由一个参数化的DNN输出,然后一样地和Di权值共享,一样地对连续分布,看成高斯分布,不一样的是,Qi仅输出均值,而方差给定。
问题:为什么这样一来,最后说LGient等价L2重建误差?
InfoGAN
简述 InfoGAN。
latent space 由noisez和 latent codes c组成,通过生成器得到G(z,c)。
如果不加限制,G容易忽略c的影响,idea是计算互信息量:I(c,G(z,c))。
I(c,G(z,c))=H(c)−H(c∣G(c,z))
互信息量的含义是:已知G(c,z)的情况下c的信息量(信息熵)和未知时的信息量减少的多少。我们希望,对任意一张生成图片,它很明显具有某种latent code编码的特性,也就是使得H(c∣G(c,z))尽可能小,所以要互信息量大。
如何将互信息量加入训练?先验分布P(c∣x)难以计算,使用Variational Information Maximization的方法用另一个Q(c∣x)得到它的下界:
I(c,G(z,c))≥Ex∼G(z,c)[Ec′∼P(c∣x)[Q(c′∣x)]]+H(c)=L1(G,Q)
当P=Q时取等号,而且I(c,G(z,c))取最小值。给定c的分布不变,H(c)为固定的常数,只需要优化加号的左项。
整个Loss:
G,QminDminV(G,D)−λL1(G,Q)
实现
D和classifier权重共享,除了最后一层不同。D输出binary结果。classifier对每一个控制的ci,如果ci是离散的变量(给定的分布也是离散的),通过softmax得到Q(ci∣x)。如果ci是连续的变量(给定的分布也是连续的),直接把Q(ci∣x)看成一个可分解的高斯变换,也就是输出两个数表示均值和方差。
实现的Codes
References
- Xun Huang, Yixuan Li, Stacked Generative Adversarial Networks.