论文阅读： GANSpace： Discovering Intrepretable GAN controls

本周阅读的文献是：“GANSpace： Discovering Intrepretable GAN controls”。

本文作者提出用PCA寻找latent space上有意义的语义变换方向，对以StyleGAN和BigGAN为代表的两类模型分别提出了对 ${\mathcal{W}}$ 隐空间分解和输出激活分解的方法，然后对得到的主成分方向的语义进行了定性分析。最后作者提出了一种比较novel的Layer-wise Edit方法，使得BigGAN可以像StyleGAN一样通过不同层注入的噪声改变输出的图像的不同尺度的细节。

上周回顾

2、在作者的代码中，求解 ${\arg \min_{z} \mathcal{L}(G(z), T_{\delta_{n}}(I_0))}$ 使用的是固定次数的梯度下降方法（使用Adam），而限制 ${\|z\| \leq \sqrt{d}}$ 的方法是每迭代一次clip ${z}$ 二范数。

3、4、 首先作者并没有对初始值的影响做定量分析。这里我有一个表述不清晰的地方，初值对求解的影响在于：采用随机初始化可能使得收敛变慢，在 Appendix D中，作者分析优化的问题在于：在图像流形上，如果初始化的 ${G(z)}$ 和目标 ${I_{target}}$ 离得比较远，会使得重建误差对隐变量 ${z}$ 的梯度较小。

梯度可以表示为：

{ \nabla_{z} \mathcal{L}(G(z), T_{\delta_{n}}(I_{target})) = \nabla_{G(z)} \mathcal{L}(G(z),T_{\delta_{n}}(I_{target})) \frac{\partial G(z)}{\partial z} }

而这两个梯度对于一些变换（如平移、放缩、旋转等）是比较正交的，如图1所示。在流形上做图像变换从 ${I}$ 到 ${I_{target}}$ 真实变化方向对应黑实线，而重建误差对图像的梯度沿着误差下降最快的方向。

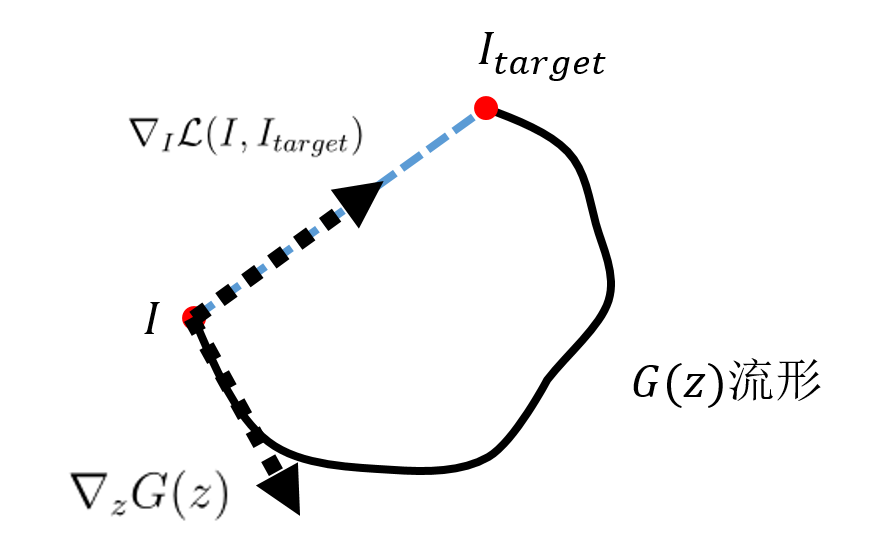
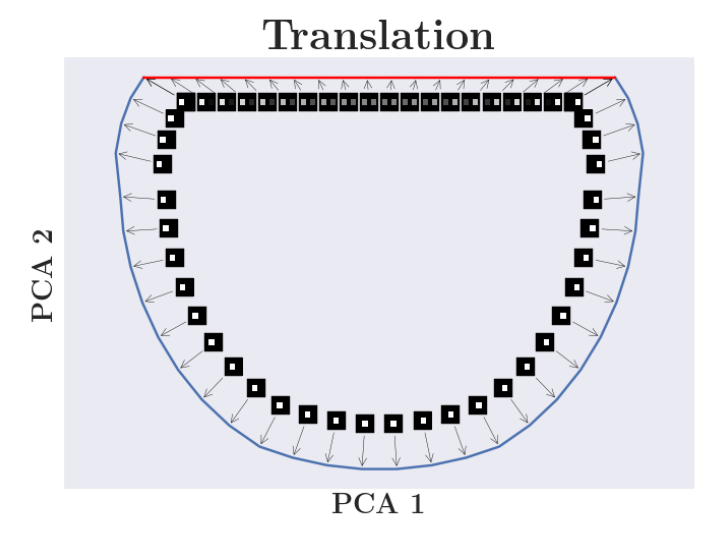
至于为什么两种方向会正交，作者是通过dSprites数据集上两图像 intepolate 方向和实际变换方向可视化得到的经验性结论，如图2，采用迭代的方法，可以使得重建误差对图像的梯度更加贴近图像流形，梯度更大，但是定量的结论还暂时没有。

5、6、
作者对于 ${g}$ 选择为分段线性函数的表述比较模糊，我猜测 ${g}$ 设置为分段线性函数的原因有：
(1) 有可能 ${\langle \vec{u},\mathbf{z} \rangle}$ 和变换程度 ${\delta}$ 不是完全的线性关系，当 ${\langle \vec{u},\mathbf{z} \rangle}$ 比较大时，受变换限度的影响， ${\delta / \langle \vec{u},\mathbf{z} \rangle}$ 变换程度会下降。
(2) 分段线性函数是更大的函数族，不但优化简单，而且引入非线性。

但是实际上，“分段线性”函数g在代码中是这样实现的：

{ f(x) = clip(x, -\epsilon, \epsilon) = \left\{ \begin{aligned} \epsilon \qquad& x > \epsilon \\\\ x \qquad & -\epsilon \leq x \leq \epsilon \\\\ -\epsilon \qquad& x < \epsilon \end{aligned} \right. }

${p_{i} = \text{linspace}(min,max,lsize)}$ 是区间 ${[min,max]}$ 上等距的点。 g的输入 ${x = \langle \vec{u},\mathbf{z} \rangle}$ 是标量，整体的计算公式为：

{ g(x) = \sum_{i} w_{i} f(x - p_{i}) }

${g}$ 的选择上确实比较奇怪，也没有任何的先验知识（百思不得其解，这还是一个残留的问题）。训练 ${w_{i}}$ 和 ${\vec{u}}$ 是一个回归问题，根据作者得到的数据集 ${(z_0, z_{\delta_n},\delta_n)}$ ， ${\delta_n}$ 是 ${z_0}$ 和 ${z_{\delta_n}}$ 的变化差的形式，所以变为差分的形式训练，具体的方式还是梯度下降。

{ \theta^{\ast}, \vec{u}^{\ast} = \arg \min_{\theta, \vec{u}} MSE(f_{\theta,\vec{u}}(z_{\delta_t}) - f_{\theta,\vec{u}}(z_{0}), \delta_n) \qquad s.t. \|\vec{u}\| = 1 \qquad g_{\theta}(0) = 0 }

9、10、 我更倾向于文章的目的是探索pretrained GAN的latent space的语义性。而图像变换是在寻找到变换语义对应的latent space上的方向的应用。

将真实图像映射到latent space，在latent space上修改再通过生成模型得到修改后的图像是一种这种方法的应用（之前阅读的文章InterFaceGAN就有关于这个的实验），这种方法相比图像处理方法可能的优点有：(1) 可以进行语义编辑。(2) 在图像进行Zoom，平移等操作后，会出现undefined的区域，传统的方式是使用reflection padding等方法填充，而该方法不需要，undefined区域会更加真实（有点类似图像遮挡修复）。

PaperFrame

引言：介绍全文工作
相关工作：现有"control GAN in latent space"的方法总结和对比
方法：
- 针对 StyleGAN 代表的模型，采用对 ${\mathcal{W}}$ 空间分解的方法。
- 针对 BigGAN 代表的模型，采用对激活分解的方法。
主成分方向语义分析
Layer-wise Edit 和它在 BigGAN 上的应用。

作者同样观察到了不同class物体可以共享相同的语义变换的latent space上的方向。所以本文的意义之一在于寻找到和语义变换有强相关性的latent space方向，然后可以迁移到其他图片上，达到语义编辑的目的。

Methods

为方便后文说明，作者先对GAN的generator的公式改写，将generator的每层记作 ${G_{i} (i = 1, \cdots, L)}$ ，该层激活输出可以表示为：

{ \mathbf{y}_{i} = \hat{G}_{i}(\mathbf{z}) \equiv G_{i}(\mathbf{y}_{i-1}) }

BigGAN的各层激活输出表示如下，BigGAN还有通过Conditional BatchNorm输入的class conditional的信息，训练时固定class，作者在公式中省略了这一项。

{ \mathbf{y}_{i} = G_{i}(\mathbf{y}_{i-1}, \mathbf{z}) }

StyleGAN的各层激活输出表示如下：

{ \mathbf{y}_{i} = \hat{G}_{i}(\mathbf{z}) \equiv G_{i}(\mathbf{y}_{i-1}, \mathbf{w}) \qquad \text{with} \qquad \mathbf{w} = M(\mathbf{z}) }

PCA

对StyleGAN类的GAN，直接对 ${\mathcal{W}}$ 进行PCA分解：

随机采样 ${z_{1:N}}$ ，得到 ${\mathcal{W}}$ 空间上的点 ${w_{1:N}}$ ，对 ${W}$ 进行分解，得到主成分矩阵 ${\mathbf{V} \in \mathbb{R}^{K \times C}}$ （ ${K}$ 表示主成分数量, ${C}$ 表示 ${\mathcal{W}}$ 空间的维数。）然后可以用以下的公式直接控制 ${w}$ 的主成分的修改，其中 ${x}$ 是可控参数：

{ \begin{aligned} \mathbf{w}^{\prime} &= \mathbf{w} + \mathbf{V} x \\\\ I &= G(y_{0}, \mathbf{w}^{\prime}) \\\\ \end{aligned} }

BigGAN类的Generator，没有StyleGAN的 ${W}$ 隐空间。作者对各层输出激活进行PCA分解。idea是：首先对激活找到主成分方向 ${v}$ （不同的样本的激活在 ${v}$ 上的投影即为主成分，也是它们在 ${v}$ 上的坐标），然后在latent space找到一个方向 ${u}$ ，latent space在 ${u}$ 的坐标变换 align with 激活在 ${v}$ 上的坐标。（ ${u}$ 的求解变成回归问题）

问：为何不在latent space上分解，不直接对图片分解？

答：因为 ${p(z)}$ 是各项同性的高斯，它本身不包含生成模型的任何信息，没有被学习，而已经固定死了分布形式。而我们需要一个东西参数化输出的图像。

随机采样 ${z_{1:N}}$ ，得到某一层的激活输出 ${y_{1:N} = \hat{G}_{i}(z_{1:N})}$ ，对 ${y_j}$ 进行PCA分解，得到主成分 ${v}$ ,计算均值 ${\mu}$ ,计算激活值在主成分方向上的投影坐标 ${x = v^{T}(y - \mu)}$ :

对单个主成分方向 ${v_{k}}$ ,激活值对应的坐标为 ${x^{k}_{1:N}}$ , 求解以下回归问题，得到latent space上对应的方向 ${u_{k}}$ ：

{ \begin{aligned} \mathbf{u}^{k} = \arg \min \sum_{j} \| \mathbf{u}^{k} x_{j} - \mathbf{z}_{j} \|^{2} \end{aligned} \tag{Equation:biggan1} }

对所有主成分，问题变成求解一个矩阵 ${U}$ ，矩阵的每一行代表一个latent space上的主成分方向:

{ \begin{aligned} \tag{Equation:biggan2} \mathbf{U} = \arg \min \sum_{j} \| \mathbf{U} \mathbf{x}_{j} - \mathbf{Z}_{j} \|^{2} \end{aligned} }

${\mathbf{U} \in \mathbb{R}^{k \times d}}$ , ${k}$ 表示主成分数量， ${d}$ 表示latent space ${\mathcal{Z}}$ 的维数。同样的，可以使用以下公式控制 ${\mathcal{Z}}$ 上主成分的变化：

{ \begin{aligned} \mathbf{z}^{\prime} &= \mathbf{z} + \mathbf{U} \mathbf{x} \\\\ I^{\prime} &= G(\mathbf{z}^{\prime}) \end{aligned} }

主成分定性语义分析

对分解的PCA主成分方向对应的语义变换，作者得到的定性的结论有：

最大的几个主成分控制尺度大的变化，如性别、物体位置，视角等。接下来的主成分控制尺度小的变化。
BigGAN 的实验得到的部分主成分可以跨类别，通常是大的主成分，如物体位置。
主成分可控的质量、泛化性受数据集所限。

Layerwise-Edit

Layewise-Edit针对StyleGAN和BigGAN这种在Generator的多层注入噪声的模型。方法是仅在部分层注入在主成分方向变化的噪声， ${\text{E}(u_{i},\text{j - k})}$ 表示仅对 j 到 k 层，注入修改主成分 ${u_{i}}$ 后的噪声。

作者在StyleGAN上观察到的定性的结论有：

1. 即使对同一种主成分，在不同层修改会引起生成图像的不同的语义变化。如 ${\text{E}(u_{1},\text{all})}$ 会同时改变头部转向、性别，而 ${\text{E}(u_{1},\text{0-2})}$ 看起来仅改变头部转向。这可能说明 disentangled 问题和模型结构也存在关系，在forward过程中，一些层会将disentangled的语义编码成 entangled 的语义。

2. 这种基于改变主成分的语义修改方法依赖于原图像的某些属性。如“胡子”主成分仅对男性的图像有用。这一点应该和训练集有关。

3. 靠后（方差占比小）的主成分可变化范围（变化显著范围）越大。这也许是因为这些主成分本身对隐编码的影响就偏小，相应地可变化范围就增大了。

BigGAN 会在不同的层注入噪声 ${z}$ 。作者使用同样的方法成功地对BigGAN也做到了layer-wise 编辑。只是得到的主成分代表的语义更 disentangled，原因是隐空间 ${\mathcal{Z}}$ 本身就不如 ${\mathcal{W}}$ disentangled。

评价

Weakness

1. 主成分随机性：本文虽然揭示了一种分解方法，但是不能得到指定语义变换的主成分，对主成分代表的语义的理解还要经过定性定量分析才能得到。

2. 主成分代表的语义 entangled 问题没有解决。

3. 激活输出和原始的 ${z}$ 是非线性关系，在求解公式(Equation:biggan2)时使用的是线性模型，
该方法能否得到比较准确的隐空间上的主成分方向存疑。

4. 本文算是一篇未完成的作品，实验上还基本上没有定量的分析，实验部分比较薄弱。

可以借鉴的地方、优点、潜在的假说：

1. 比起同类“control GAN in latent space”的方法，本文提出的方法是无监督的（基于PCA分解）。

2. StyleGAN 的 layer-wise edit定性实验可能说明了 disentanglement 问题和模型结构存在一定的关系。

这篇文章可以看作是探索pretrain-GAN 隐空间语义性的工作。具体点说，这篇文章探索的是 Generator 在forward隐编码时关注的变换，这种变换由于 Generator 训练地越好，越可能和某种 disentangled 的语义属性关联地越好（有工作认为，训练地好的GAN自身已经学习到了disentangled representation），但是本质上我并不认为它是专门针对语义的 disentangled 表示的工作。