每日文章： Adversarial Latent Autoencoders

Preface

A Paper A Day Keep the Doctor Away. 今天的文章是：

Adversarial Latent Autoencoders. [paper] [codes] (CVPR2020)

本文的ALAE在github上挺热门的，思路其实也挺简单的，有值得令人深思的地方。

Main Contents

ALAE Architecture

ALAE的模型架构有三点：

(1) 把GAN原有的Generator和Discriminator分别拆分成 ${G = G \circ F, D = D \circ E}$ ，如图1所示。

(2) 将更改后的 ${G,E}$ 变成stochastic的， ${G}$ 的输入增加一个已知分布的 ${\eta \sim p(\eta)}$ 噪声 ${\eta}$ ，输出为 ${G(w, \eta)}$ 。

(3) Impose latent space matching，即使得 ${F}$ 输出的 ${\mathcal{W}}$ 空间和 ${E}$ 输出的 ${\mathcal{W}^{\prime}}$ 空间的分布相同。

最终的架构如图1所示，而相应的Loss变为：

{ \begin{aligned} \min_{F,G} \max_{E,G} V(G \circ F, D \circ E) \\ \min_{E,G} \Delta(F \| E \circ G \circ F) \end{aligned} }

其中：

{ V(G,D) = \mathbb{E}_{p_{D}(x)} [f(D(x))] + \mathbb{E}_{p(z)} [f(-D(G(z)))] }

当 ${f(t) = t}$ 时为WGAN，当 ${f(t) = -\log ( 1 + exp(-t)) }$ ，即log(sigmoid)时，为原始GAN。

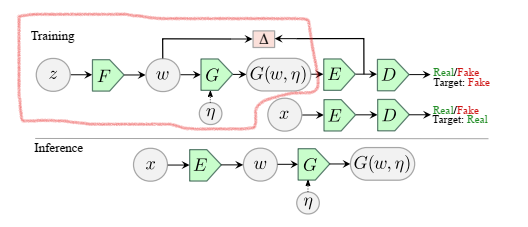
模型可以有两种Inference：(1) Unconditional Generation:如图中红线包含区域，直接使用Generator。(2) Style Reconstruction: 图中标注的Inference阶段，对图像进行Style重建。

作者还讨论了ALAE和之前一些方法的对比，如图2所示：

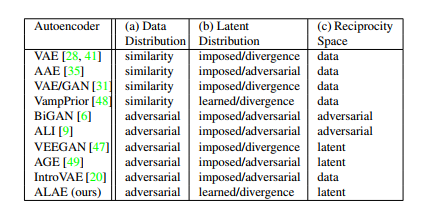
Data Distribution 指的是为了促进 ${p_{model}(x)}$ 和 ${p_{data}(x)}$ 匹配所使用的方法。部分基于VAE的方法如VAE、AAE等是使用ELBO中的L2范数度量重建图像和原始图像的相似度的方法（称为similarity）。而基于GAN的方法一般是用G和D优化 ${\text{JS}(p_{model}(x) \| p_{data}(x)) }$ （称为adversarial）。很明显ALAE是基于GAN。

Latent Distribution 指的是隐编码的分布 ${q(z)}$ 的优化。一部分基于原始VAE的方法，是设定好先验 ${p(z)}$ 的形式（称为imposed），如常见的标准高斯，并且优化二者的散度（称为divergence），如KL散度。而类似AAE的方法，将二者散度的优化变成了GAN的minmax game（称为adversarial）。VampPrior使用的是可学习的先验（称为learned）。本文的ALAE，作者认为模型不需要设定先验形式，而且优化公式表明优化divergence。（但是我感觉，作者就用了L2-norm作为优化公式中的 ${\Delta}$ ，在分布形式都没给定的情况下这算啥divergenece优化？）

Reciprocity 指的应该是达到Encoder和Decoder的可逆性。可以是对图像重建，也可以是对隐编码重建，即 ${x^{\prime} = D(E(x))}$ 或者 ${z^{\prime}=E(D(z))}$ 。显然ALAE是后者。 BiGAN和ALI的方法不太了解，暂时不太了解impose reciprocity adversairally的方法。

StyleALAE

作者将ALAE扩展到类似StyleGAN的形式，具体来说就是修改了ALAE中G和E的形式。 G换成StyleGAN的架构，而与之相对的设计了一种新的Encoder架构，如图3。

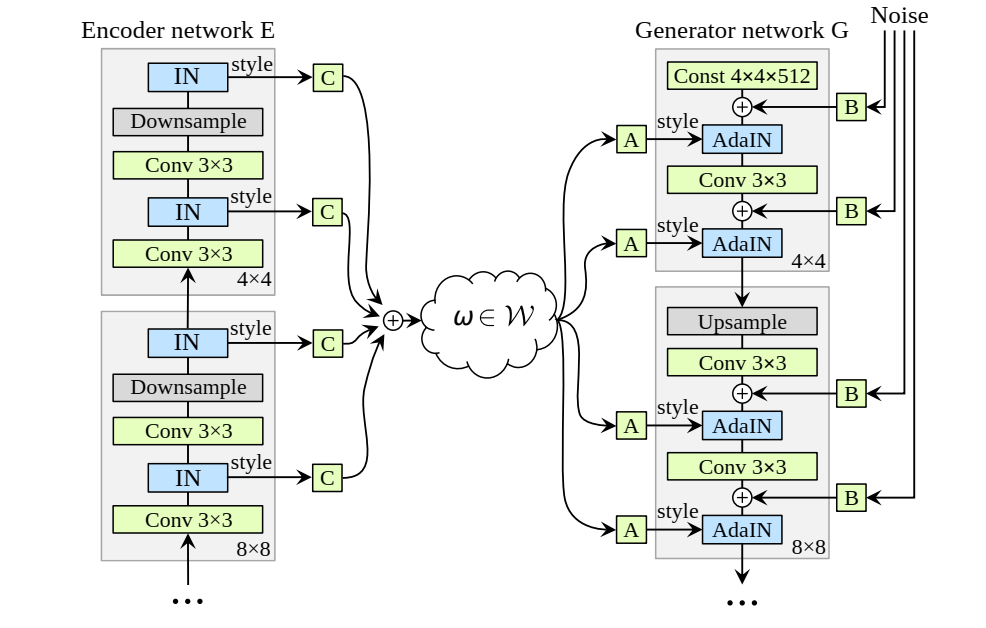
Encoder差不多可以看成G的逆过程，不过是每个Style Level上使用IN提取均值和方差作为style。而最终 ${\mathcal{W}}$ 的输出为加权加总：

{ w = \sum_{i = 1}^{N} C_{i} \left[ \begin{matrix} \mu(y_{i}^{E}) \\ \sigma(y_{i}^{E}) \end{matrix} \right] }

其中 ${C_i}$ 可学习。

另外，和PGGAN一样训练使用Progressive Growing的方法。而对于 ${F}$ 和 ${D}$ ，它们的复杂性比较低，直接使用MLP，特别地， ${F}$ 和StyleGAN一样取8层的MLP。

Implementation

实现上值得注意的有两点：

(1) 作者取 ${f(t) = \text{softplus}(t) = \log(1 + exp(t)) }$ 。

(2) Gradient Penalty项 ${\frac{\gamma}{2} \mathbb{E}_{p_{D(x)}} [ \| \nabla D \circ E(x) \|^{2}] }$ 。

这两点我还没看过相关文献，所以具体作用还不懂哈哈，参考[1,2,3]。

训练过程如图4，就是按照目标loss，依次train。但是全文不见 ${\eta}$ 不奇怪吗？😃

实验

作者在MNIST上构建了MLP-ALAE，在LSUN, FFHQ, Celeb-HQ上构建StyleALAE实验。值得关注的实验结论：

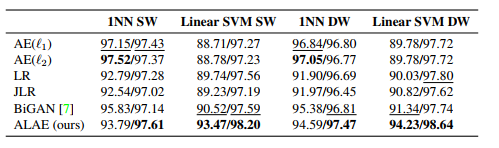
(1) MNIST上MLP-ALAE的表示分类实验中，long feature(Encoder最后一层输入)，short feature( ${\mathcal{W}}$ 上的表示)：虽然没有取得一致的最好表现，但是作者认为 1NN到Linear SVM的切换表现更稳定，认为ALAE的disentanglement表现更好。但是我觉得看起来大家的差距也不太大，说服力不强。

(2) StyleALAE实验：展现了比较好的Style重建、Level-Control的人脸融合、unconditional生成方面的视觉效果。 FID表现比StyleGAN差了点，但是PPL上比StyleGAN进步了不少，认为 ${\mathcal{W}}$ 比StyleGAN的更加Disentangled。

一些实验结果：

图5：MNIST上表示分类实验。使用1NN和Linear SVM分类，根据train/test的划分不同分为DW(different writer)和SW(same writer)两种，同时每个表示又使用short feature/long feature两种对比

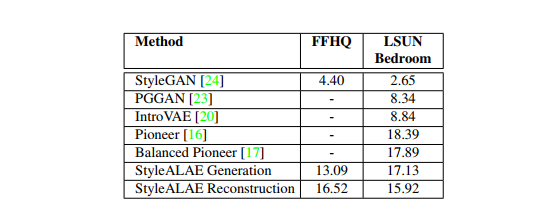
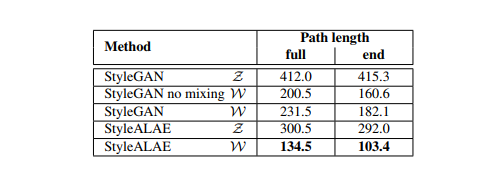
总结

本文的ALAE显然是从StyleGAN的 ${\mathcal{W}}$ 空间考虑，去添加一个Encoder和Decoder的机制。越来越多的文献表明了 ${\mathcal{W}}$ 隐空间的重要性，是个好坑。

References

Which training methods for gans do actually converge?. Lars Mescheder et.al. arXiv:1801.04406, 2018.
Stabilizing training of generative adversarial networks through regularization. Kevin Roth et.al. NIPS2017.
Improving the adversarial robustness and interpretability of deep neural networks by regularizing their input gradients. Andrew Slavin Ross et.al. AAAI2018.