基于BoW特征的图像分类(1)

prefaces

CV课的大作业，两篇论文： “Local Features and Kernels for Classification of Texture and Object Categories: A Comprehensive Study” 和 “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories”，的阅读、方法的总结以及后者的实现。

本文是第一篇论文的阅读。

总结

选题选的是“基于BoW特征的图像分类”，首先BoW特征在网上的资料也很多，主要方法就是类比NLP中的构建词库的方法，对所有特征进行一个聚类，得到词库，并且得到图像在这些特征上的直方图，根据直方图进行匹配。

论文1的阅读

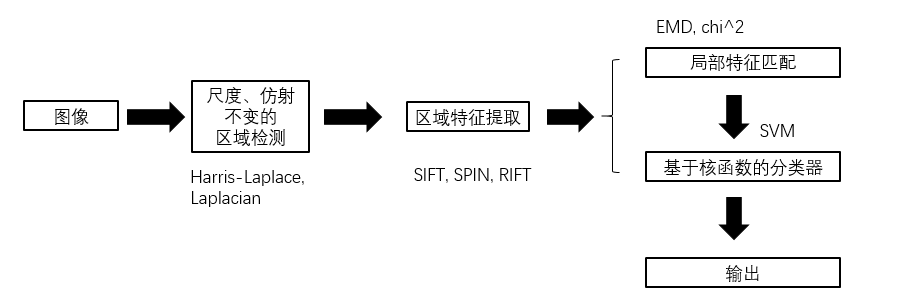
本文方法的构成包括四个要素： (1) 尺度和仿射变换不变区域检测算子； (2) 区域特征描述子； (3) 局部特征匹配方法； (4) 分类器以及核函数。方法的整体流程是：首先由检测算子检测感兴趣的区域，再由描述子提取局部特征，由局部特征匹配方法计算任意两张图像的匹配分数，再由基于核函数的分类器分类（主要是 svm）。而局部特征匹配方法是作为计算核函数的一部分，可以将 (3)(4) 合并。

尺度和仿射变换不变区域检测算子

首先要对图像感兴趣的区域检测，本文关注尺度不变、旋转不变、仿射不变三种特性。

尺度不变：
本文选取的是 Harris-Laplace 和 Laplacian 检测算子，分别对角点区域、联通区域检测，而本身两种检测算子本身满足尺度不变的特点。

旋转不变： 本文采取了两种方法，一是使用旋转不变的特征描述子，SPIN 和 RIFT，二是将圆形区域旋转到主梯度方向，并取主梯度方法为区域内所有梯度之和。

仿射不变： 使用仿射适应修正梯度算子。

区域特征描述子

区域特征提取上，本文选取了三种描述子： SIFT, SPIN 和 RIFT。

SIFT描述子： 计算支撑区域的梯度方向直方图。具体而言，在 4x4 的子块上，统计八方向梯度的直方图，共计128维特征，并将同方向的梯度累积，最后累积还要对区域内不同位置的梯度取权重，权重是该位置到区域中心的L2距离取标准高斯。使得靠近中心的梯度更大。

SPIN描述子： 基于 spin image，构造支撑区域内旋转无关的二维的强度的直方图。直方图的两维度分别是点到区域中心距离 ${d}$ 和点的强度 ${i}$ 。 ${(d, i)}$ 的值就是距离中心为 ${d}$ 强度为 ${i}$ 的点的出现概率。本文实现中两个维度的 bins 都取 10 个，共计 100 维特征。

RIFT描述子： 旋转不变版本的SIFT，构造的也是梯度方向直方图。具体来说，它将区域划分为等宽的同心环区域，在环内统计八方向梯度直方图。而梯度方向是相对点和中心连线的相对方向。取 4 个环，共计 32 维特征。

其次为了使得特征对光照无关：对SPIN, RIFT：计算特征前用区域强度的均值和方差对区域作归一化处理。而对RIFT：将特征的范数放缩到 1。

最后，在本文实验中，将不同检测算子和不同描述子结合，得到不同的特征，作为一个特征的通道，使得可以使用融合特征分类。

局部特征匹配方法

以上两步获得描述子特征之后，考虑基于局部特征分布的图像相似度计算。本文选取了两种方法：

第一种方法是对每张图像的描述子进行聚类，得到图像的 signature: ${\left\{(p_i, u_i), \cdots, (p_m, u_m)\right\}}$ 。其中 ${m}$ 是聚类的数量， ${p_i}$ 是各类中心， ${u_i}$ 是类中特征个数。

任意两个图像的 signature: ${S_1 = \left\{(p_1, u_1), \cdots, (p_m, u_m) \right\}}$ ， ${S_2 = \left\{(q_1, w_1), \cdots, (q_m, w_m) \right\}}$ 的相似度计算用推土机距离（Earth Mover’s Distance）计算：

{ D(S_1, S_2) = \frac{\sum_{i = 1}^{m} \sum_{j = 1}^{n} f_{i,j} d(p_i, q_j)}{\sum_{i = 1}^{m} \sum_{j = 1}^{n} f_{i,j}} }

其中 ${d(p_i, q_i)}$ 是两个聚类中心的距离，本文直接使用 L2 距离， ${f}$ 是 flow value，可以求解线性规划得到。另外，推土机距离不要求 ${m = n}$ ，所以两图像的signature 长度可以不同，

第二种方法是构建全局的纹理基元词库。纹理基元词库在特殊训练集上训练聚类算法得到。通过词库可以将图像表示为纹理基元的直方图，计算直方图之间的距离。假设 ${u_i}$ 表示属于 ${i}$ 类基元的描述子特征数量占该图像的所有特征数量的比例，两个图像直方图 ${S_1 = (u_1, \cdots, u_m)}$ ， ${S_2 = (w_1, \cdots, w_m)}$ 的距离用 ${\chi^{2}}$ 距离计算：

{ D(S_1, S_2) = \frac{1}{2} \sum_{i=1}^{m} \frac{(u_i - w_i)^{2}}{u_i + w_i} }

本文将每类图像的聚类得到的 10 个纹理基元合并，得到纹理基元词库。

分类器和核函数

本文选择SVM作为分类器，对二分类任务使用 binary svm，对多分类任务，本文使用 1对1 的策略，对每一对类之间训练一个 svm，在测试阶段，使用所有分类器分类样本，并将出现次数最多的类作为样本的目标。作者实验中验证了 1对1 策略和 1对多策略效果相近。

将上节的两种局部特征匹配方法融入到核函数计算，得到核：

{ K(S_i, S_j) = \exp(- \frac{1}{A} D(S_i, S_j)) }

${D(S_i, S_j)}$ 取 EMD 或者 ${\chi^2}$ 距离得到的核分别称为 EMD 核函数和 ${\chi^2}$ 核函数。 ${A}$ 是放缩系数，本文直接取为 ${D(S_i, S_j)}$ 的均值，发现不影响结果。

另外 ${\chi^2}$ 已经被证明是 Mercer 核，EMD 核并没有相关证明，但是本文作者在实验中使用 EMD核总可以使得数据的 Gram 矩阵正定，满足 Mercer 定理。

总体算法总结

一些存在疑问的地方、或者没有查阅的地方

仿射适应修正梯度算子还没完全明白

References

[1] Jianguo Zhang, M. Marszalek, S. Lazebnik and C. Schmid, “Local Features and Kernels for Classification of Texture and Object Categories: A Comprehensive Study,” 2006 Conference on Computer Vision and Pattern Recognition Workshop (CVPRW’06), New York, NY, USA, 2006, pp. 13-13, doi: 10.1109/CVPRW.2006.121.

[2] S. Lazebnik, C. Schmid and J. Ponce, “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories,” 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 2006, pp. 2169-2178, doi: 10.1109/CVPR.2006.68.