prefaces

CV课的大作业，两篇论文： “Local Features and Kernels for Classification of Texture and Object Categories: A Comprehensive Study” 和 “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories”，的阅读、方法的总结以及后者的实现。

本文针对第二篇。第二篇的实现代码： https://github.com/MercuriXito/Spm

Bags of Feature 在将图像表示为局部特征的无序集合时，丢弃了局部特征之间的结构特征。 本文就是针对 Bags of Feature 的无序性的改进。从空间和尺度两个方面对 Bags of Features 增强。 尺度上，本文借鉴了金字塔匹配核函数(Pyramid Matching Kernel)[3] 的思路计算两个特征集合的匹配。空间上，将不同类特征的空间位置作为新特征，并且作为金字塔匹配核函数的输入，得到匹配输出。

Contents

Pyramid Matching Kernel

金字塔匹配核函数[3] 用于计算图像特征的匹配，用于计算两个特征几何的匹配，该核函数已经被证明满足 Mercel 定理，可以是 svm 的核函数。

该匹配核函数的计算如下：假定向量X,Y{X,Y}是 d 维特征空间中的两个向量集合。首先对每个维度的特征建立分辨率为l=0,⋯ ,L{l = 0, \cdots, L}的网格，第l{l}层的网格将特征划分为2l{2^{l}}段，并将d维的特征空间划分为总共 2dl{2^{d l}} 个cells。记HXl,HYl{H^{l}_{X}, H^{l}_{Y}}为在l{l}分辨率的网格中，向量集合X,Y{X, Y}的以这个 cells 为 bin 的直方图，HXl(i),HYl(i){H^{l}_{X}(i), H^{l}_{Y}(i)}就表示两个向量集合中落入第i{i}个cell 的向量数。计算这两个直方图的交作为在l{l}层的匹配数：

I(HXl,HYl)=∑iDmin⁡(HXl(i),HYl(i)){ \mathcal{I}(H^{l}_{X}, H^{l}_{Y}) = \sum_{i}^{D} \min(H^{l}_{X}(i), H^{l}_{Y}(i)) }

将I(HXl,HYl){\mathcal{I}(H^{l}_{X}, H^{l}_{Y})}简记为Il{\mathcal{I}^{l}}。

注意到第l{l}层的匹配是包括了第l+1{l+1}层的匹配，所以第l{l}层新出现的匹配数为Il−Il+1{\mathcal{I}^{l} - \mathcal{I}^{l+1}}。对每一层的匹配赋权值，并且希望越细的网格上的匹配数权重越大，取1/2L−l{1 / 2^{L-l}}，这样得到综合的匹配函数为：

κL(X,Y)=I0+∑l=0L−112L−l(Il−Il+1)=12LI0+∑l=0L−112L−l+1Il{ \begin{aligned} \kappa^{L}(X, Y) &= \mathcal{I}^{0} + \sum_{l = 0}^{L - 1} \frac{1}{2^{L-l}}(\mathcal{I}^{l} - \mathcal{I}^{l + 1}) \\ &= \frac{1}{2^{L}} \mathcal{I}^{0} + \sum_{l = 0}^{L - 1} \frac{1}{2^{L-l + 1}} \mathcal{I}^{l} \end{aligned} }

Spatial Matching Scheme

本文的空间金字塔匹配的过程如下：

先和 Bags of Features 一样构建词库，将图像的特征划分成M{M}类。两图像的每一类（m{m}）特征的点构成两个二维向量集合Xm,Ym{X_m, Y_m}，集合中的每一个向量表示该类特征点的x,y坐标。于是可以使用金字塔匹配核函数计算Xm,Ym{X_m, Y_m}的匹配程度κL(Xm,Ym){\kappa^{L}(X_m, Y_m)}，计算所有特征的匹配数，求和就得到本文的空间金字塔匹配：

KL(X,Y)=∑m=1MκL(Xm,Ym){ K^{L}(X,Y) = \sum_{m=1}^{M} \kappa^{L}(X_m, Y_m) }

可以看到，当L=0{L = 0}时，金字塔只取整个图像一层，所以此时退化成 原始的 Bags of Features 特征的匹配。

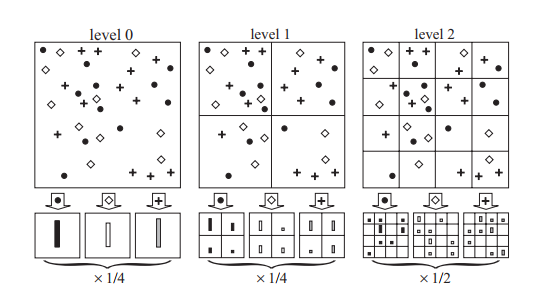
图1. 空间金字塔匹配计算
图1. 空间金字塔匹配计算

计算上，因为对正数有：cmin⁡(a,b)=min⁡(ac,,bc){c \min(a, b) = \min(ac, ,bc)}，整体公式可以变为：

KL(X,Y)=∑m=1Mmin⁡(12LHXml,12LHYml)+∑l=1L−1∑i=1Dmin⁡(12L−l+1HXml(i),12L−l+1HYml(i)){ K^{L}(X,Y) = \sum_{m = 1}^{M} \min\left( \frac{1}{2^{L}} H^{l}_{X_m}, \frac{1}{2^{L}} H^{l}_{Y_m} \right) + \sum_{l = 1}^{L - 1} \sum_{i = 1}^{D} \min\left( \frac{1}{2^{L-l+1}} H^{l}_{X_m} (i), \frac{1}{2^{L-l+1}} H^{l}_{Y_m} (i) \right) }

所以可以构建由12L−l+1HXml(i),12L−l+1HYml(i){ \frac{1}{2^{L-l+1}} H^{l}_{X_m} (i), \frac{1}{2^{L-l+1}} H^{l}_{Y_m} (i) }组成的两个长向量，两个长向量按行取最小值，最后求和。该长向量的维度可以计算得到，为M13(4L+1−1){M\frac{1}{3}(4^{L+1} - 1)}。单个向量的构建如图1所示。

总结

算法总结如图所示：

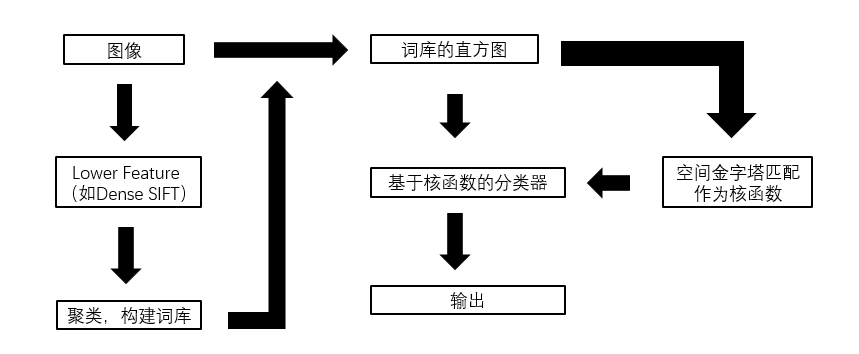
图2. 算法流程
图2. 算法流程

Implementation

本文的方法还是容易实现的，我进行了简单的实现，并在Caltech101数据集上报告了测试结果。

Caltech 数据集

Caltech101 数据集[4]是CV之前的图像识别数据集的一种，共包括 102 类物体，物体的种类比较多样，有：手风琴、剑龙、阴阳图案、谷歌标志背景等。而且每一类内的图像在大小、颜色、视角等方面也比较多样。每一类的图像从 31 张到 900 多张不等，是当时视觉任务中最多样化的数据集的一种。大部分图像是中尺寸，所以实现上
按照论文的思路，将图像统一放缩到300x300大小，并且使用灰度图作为输入。

实验细节以及实验

部分实验的细节设计和处理：

(1) 图像预处理：如上文所述，依照原文的设定，输入将图像 resize 成统一 300x300 大小。 由于作者的实验中提到用彩色图的提升不大，所以实现也仅针对灰度图。

(2) 使用 Dense sift 作为底层特征，每隔 8 个像素，以该像素为中心取 16x16 大小的 patches，计算 sift 描述子。则一张输入的图像共计 37x37x128 个特征。

(3) 考虑到特征的数量比较大，词库的聚类使用 MiniBatchKMeans，训练取batch大小为1000，并且最多采样 20000 个随机 patches的描述子进行训练。

参数如下表：

dense 区域大小 步长 聚类训练样本数 聚类batch大小 图像大小
16 8 20000 1000 300x300

其他细节参见代码：https://github.com/MercuriXito/Spm

Results

实验对词库大小M{M}，金字塔匹配层数L{L}，各类使用的训练样本大小N{N}超参数的影响进行了对比。

按照原文的设定，词库的大小M={200,400}{M = \left\{ 200, 400\right\}}，L=0,1,2,3{L = 0,1,2,3}，N=15,30{N = 15, 30}。当每类取15个样本时，每类最多取20个样本作为测试集。当每类取30个样本时，每类最多取50个样本作为测试集。限于计算资源限制，大部分实验在N=15{N = 15}时进行，N=30{N = 30}时，取相应的表现较好的M=200,L=1,2{M = 200, L = 1, 2}作为对比实验。指标选取平均的测试集的top-1准确率，和根据各类样本数加权的准确率。
实验结果如图3所示。

另外，本文没有对和本文较为无关的SVM模型的参数细调，仅使用默认参数，所以效果上不如原文的效果。

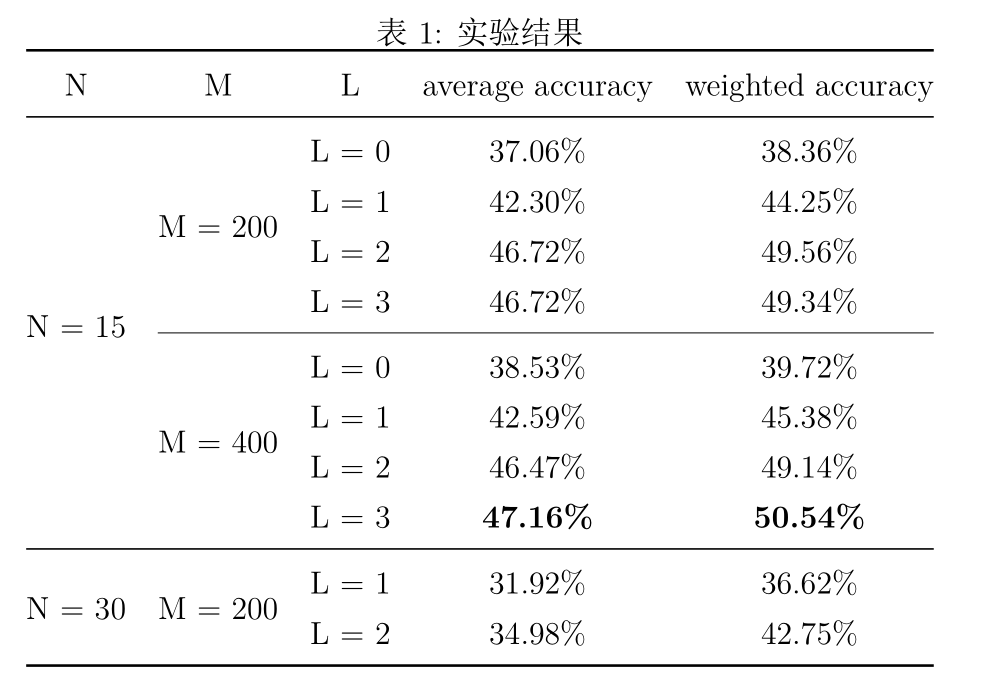
图3. Results
图3. Results

在N=15{N = 15}的实验中，M=400,L=3{M = 400, L = 3}的模型在准确率和加权准确率上都取得了最好的表现。

  • 模型的表现随着L{L}的增大而变好，说明本文方法确实有效，尤其是和L=0{L = 0}（退化成BoF特征）对比，提升较大。
  • 从训练效率来看，L{L}越大，计算时间增加地越多（向量长度呈指数级增长），而且L=3{L = 3}较L=2{L = 2}的提升也不大，选择L=2{L = 2}是比较好的选择。
  • 模型的表现随着M{M}的增大略有提升，但是基本不大（也可能是误差），所以M=200{M = 200}已经足够，这个结论和原文同样一致。

除此之外，N=30{N = 30}的模型较N=15{N = 15}的模型差的比较多，一是因为N=30{N = 30}时，测试集的样本也更多，第二个可能的原因是，N=30{N = 30}时，测试集内各类样本的比例更不平衡，部分类样本少于50，甚至只有30多个样本，相比之下，N=15{N = 15}时，总共取 35 个样本，各类数据更平衡。

References

[1] Jianguo Zhang, M. Marszalek, S. Lazebnik and C. Schmid, “Local Features and Kernels for Classification of Texture and Object Categories: A Comprehensive Study,” 2006 Conference on Computer Vision and Pattern Recognition Workshop (CVPRW’06), New York, NY, USA, 2006, pp. 13-13, doi: 10.1109/CVPRW.2006.121.

[2] S. Lazebnik, C. Schmid and J. Ponce, “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories,” 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 2006, pp. 2169-2178, doi: 10.1109/CVPR.2006.68.

[3] Kristen Grauman and Trevor Darrell. The Pyramid Match Kernel: Discriminative Classification with Sets of Image Features. (ICCV’05)

[4] L. Fei-Fei and P. Perona. A bayesian hierarchical model for learning natural scene categories. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), volume 2, pages 524–531 vol. 2, 2005.